三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方 三平方の定理 基礎数学 基礎数学 ピタゴラス ピタゴラスの定理 三平方の定理、三平方 計算 設計・計算ポータルサイトカーナビはなぜ正確なの? その秘密、「三平方の定理」で教えます 折り紙を使った簡単な証明も! 動画あり 横山 明日希 プロフィール また
Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau
三平方の定理 計算 エクセル
三平方の定理 計算 エクセル-三平方_三辺の長さから三角形の面積を求める 三辺の長さがわかっている三角形の面積の出し方。 三平方の定理を利用して 方程式 をつくり、高さを求める。 ABCの面積を求めよ。 9cm 10cm 11cm A B C If playback doesn't begin shortly, try restarting your device Videos you watch三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れて




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
それで、三平方の定理を使えば、 2× 2 =√3×√3+ 1 × 1 になることは納得できます。 そのため、次の内容は正しいことになります。 3 つの辺が√3と 2 と 1 の三角形は直角三角形になり、内側の角度は 90 度、 60 度、 30 度になる このことは三平方の定理三平方の定理とは? 下図1のような直角三角形ABCの3つの辺abcには、次のような式が成り立ちます。 ① (斜辺の2乗は他の2辺の2乗の和に等しい) これを三平方の定理といいます。 三平方の定理の計算方法 図1の3つの辺abcを三平方の定理を使って求めてみ初等幾何学における ピタゴラスの定理 ( ピタゴラスのていり 、 ( 英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理 ( さんへいほうのていり ) 、 勾股弦の
三平方の定理(ピタゴラスの定理)の計算プログラムです。 三平方の定理 直角三角形の3辺の長さがそれぞれ a, b, c で、かつ斜辺が c のとき、 a 2 b 2 = c 2 が成り立つ。 2辺を入力すると残りの1辺を求めます。 分数・根号の入力が可能です。 三平方の定理(基礎) 中3数学 直角三角形で2辺の長さがわかれば三平方の定理でもう1辺の長さが出ます。 定理に当てはめて計算するだけですが、ルートの計算を慎重に行ってくださいね。 今回は基本ですが、しっかり練習して慣れ三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x > 0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。
三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




三平方の定理の逆ってなに どうやって証明するの 数スタ
三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a b 三平方の定理を使って三角形の計算をします。 かんたん計算機 三平方の定理 計算機 「ご注意計算結果について、正確な結果が出るように検証をしていますが、間違いがある可能性もあ



3



三平方の定理
三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2三平方の定理は、もとの直角三角形を二つの直角三角形に分けて、二組の相似を見つけることで証明する。 中学数学 中3数学 中3数学 図でよくわかる三平方の定理(ピタゴラスの定理)の証明と計算問題 三平方の定理を使うときの計算の工夫を教えたいと思っております!! 三平方の定理はわかりますよね? 直角三角形の3辺の長さの関係を表した定理です。 ピタゴラスの定理とも言います。 わからない人のために写真を




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月
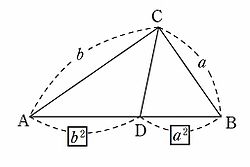



ピタゴラスの定理 Wikipedia
合法的に三平方の定理を使うコツをご紹介したいと思います。 正方形の一辺を cmとすると、赤線を斜辺とした直角三角形で三平方の定理を使用して × +3× ×3× =100 10× × =100 × =10 求める面積は面積10cm^2の正方形5つ分なので 10×5=50 A50cm2 コツは × の三平方計算21 三平方の定理で辺の長さ,高さや表面積,体積,最短距離を求める問題 印刷機能有 koya7シリーズ三平方の定理は、別名『ピタゴラスの定理』と呼ばれます。 ピタゴラスは確か大昔の数学者です。 世界的にもこの定理は有名ですので少し解説していきたいと思います。 » この記事の続きを読む これで計算するのが楽しくなるかもしれませんよ。




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
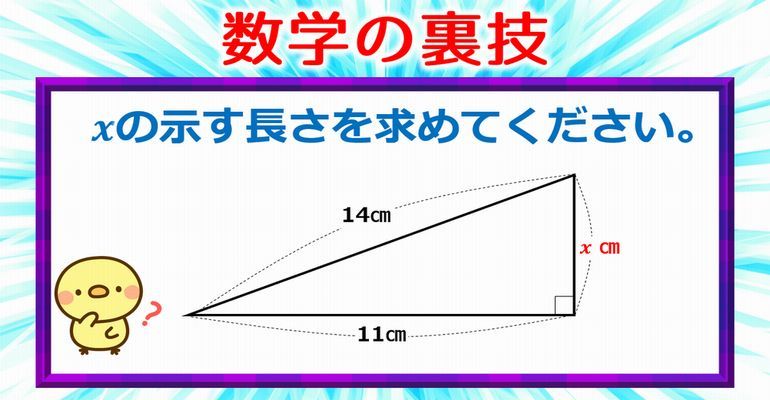



数学の裏技 デキる人はやっている三平方の定理をラクに計算する方法 子供から大人まで動画で脳トレ 楽天ブログ
14 三平方の定理の計算のために、復習しておくとよい内容 15 三平方の定理の証明(中学生にもわかりやすい) 16 特別な直角三角形4つ(角度や比を覚えておくと入試・受験でラクできる三平方の定理 自動計算サイト 三平方の定理による辺の長さの計算です。 三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に




三平方の定理について考える3 文教出版巻末の 数学研究室 より 身勝手な主張



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau
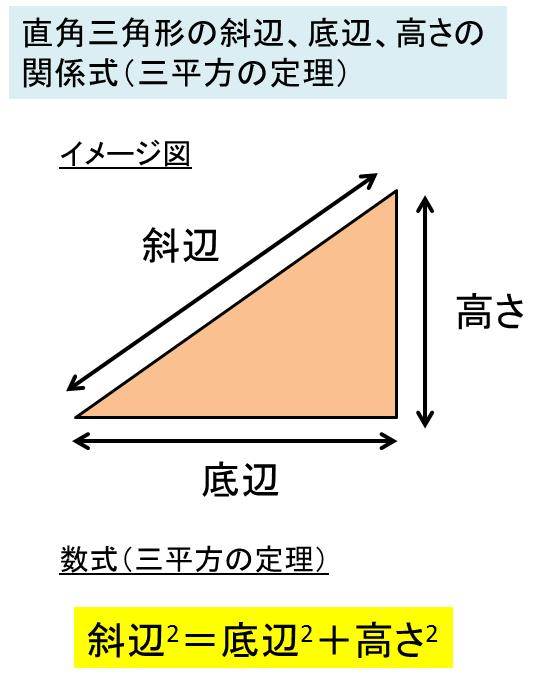



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方
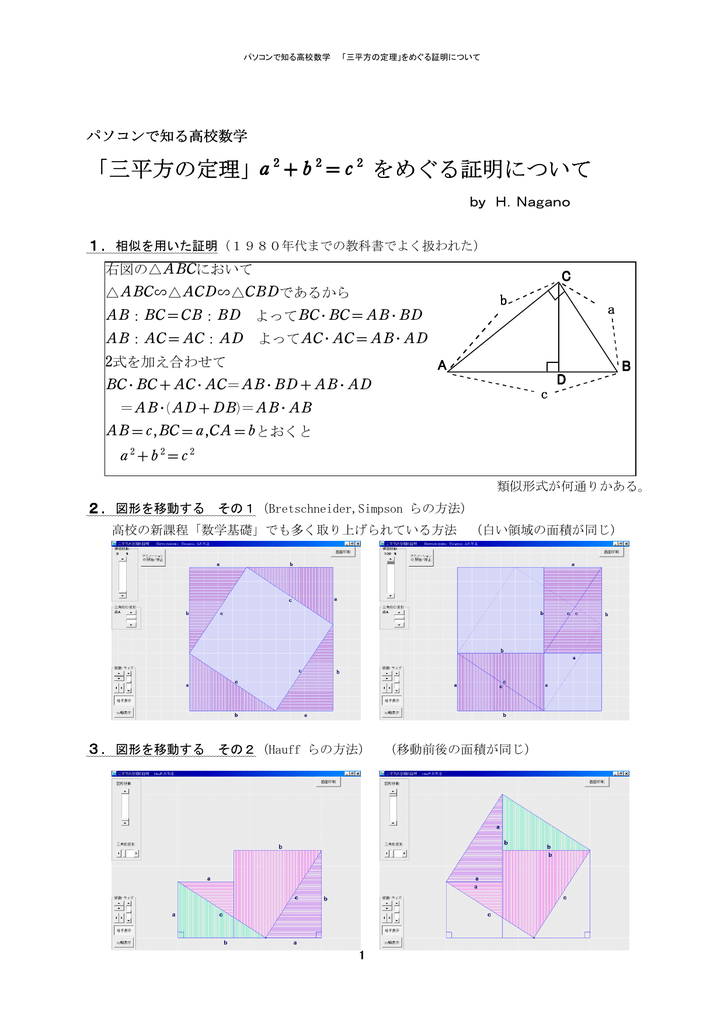



Sanheihou Theorem




三平方の定理 自動計算サイト




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




中学校 中学生の範囲で三平方の定理を証明 よく出る4パターン



1
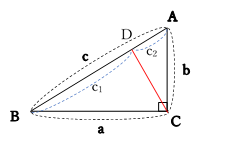



三平方の定理 おやじさん ネット




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
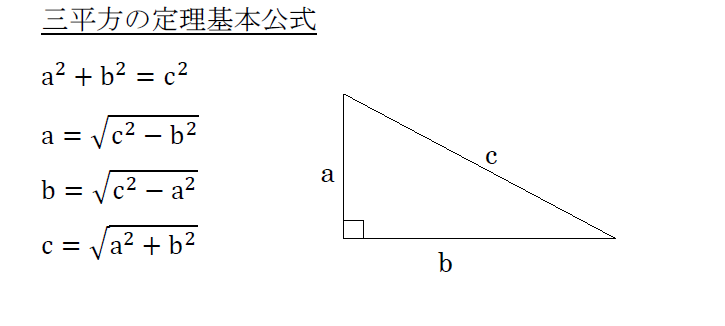



受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4




数学を愛する会 本発売 三平方の定理の証明 物理




中学数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ
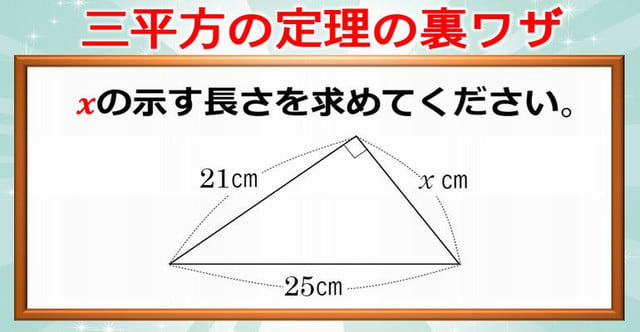



三平方の定理の裏ワザ 賢く解きたい計算の裏ワザ 暇つぶしに動画で脳トレ




三平方の定理で辺を求める Youtube
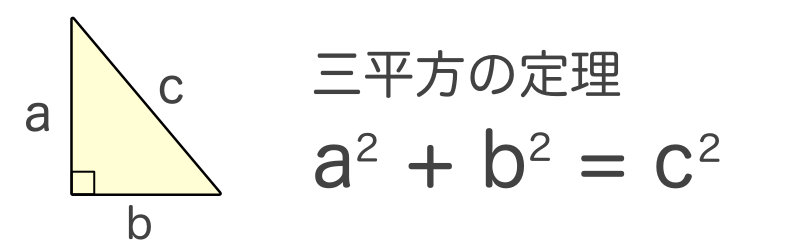



三平方の定理 簡単に計算できる電卓サイト
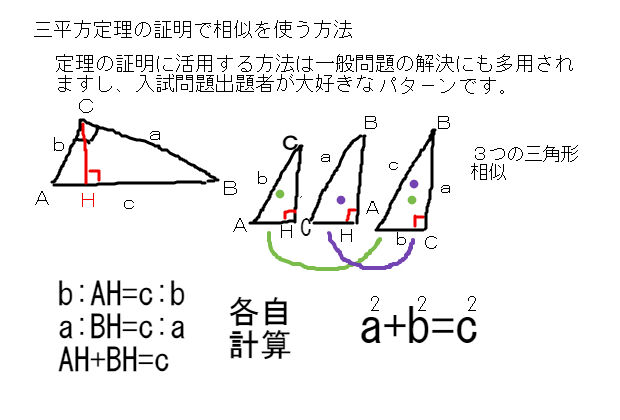



三平方定理の証明内容で最も覚えておくべきこと 中学数学 理科 寺子屋塾の復習サイト
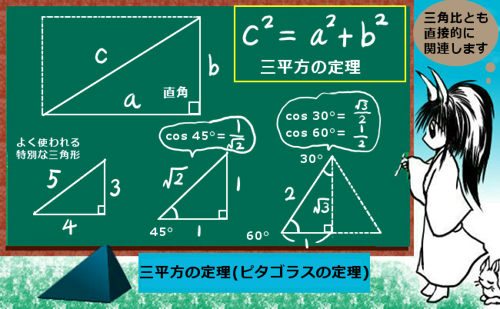



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori
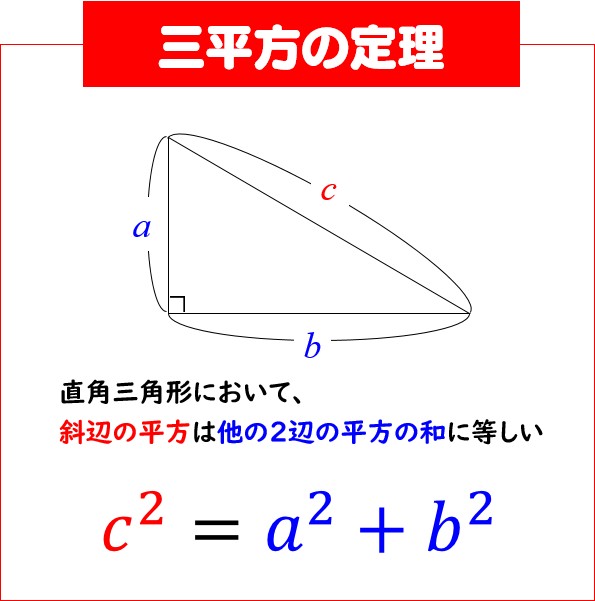



三平方の定理の証明 直感的に分かる図で解説します 数学fun



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Pc Mathekyouzai001 Sanheihou Theorem Pdf



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
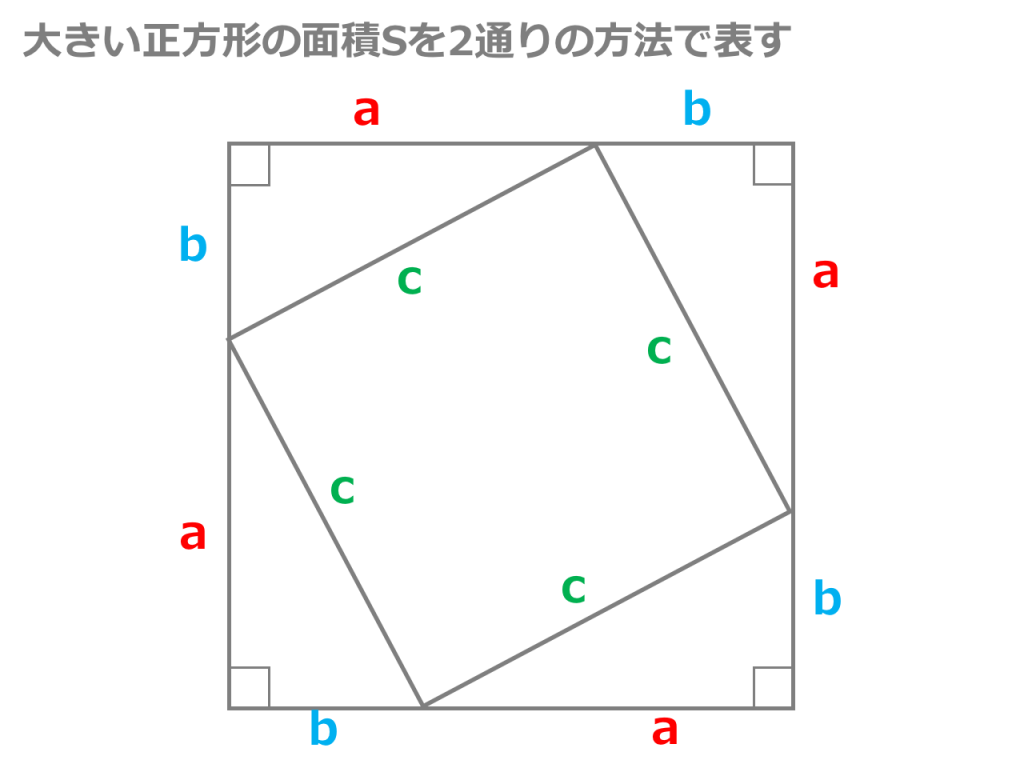



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




てなぐさみのメモ 三平方の定理と素因数分解と円の接線




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
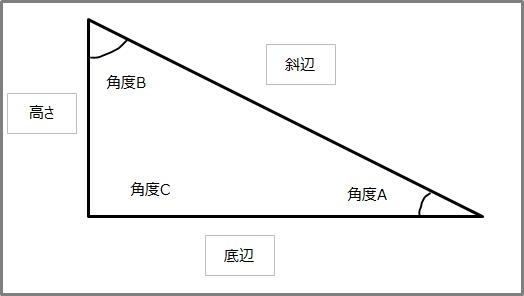



三平方の定理の計算 角度と長さ Nujonoa Blog




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト
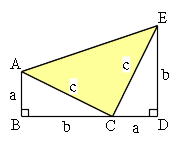



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理の計算工夫 勉強を頑張っている人のための勉強法
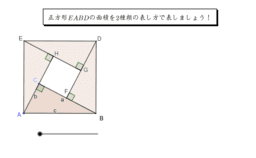



三平方の定理 Geogebra




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学



三平方の定理から円周率を計算してみる Yamav1 02bのブログ




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学
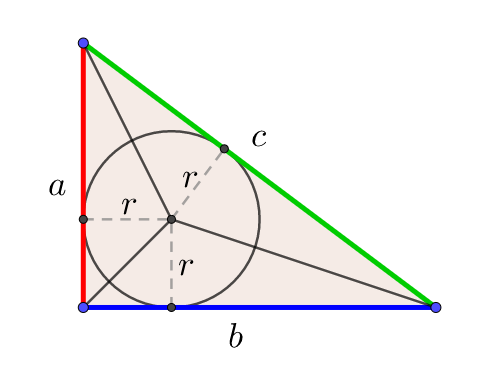



三平方の定理の証明4 直角三角形と内接円 キソカラ




三平方の定理の4通りの美しい証明 高校数学の美しい物語




三平方の定理 よく使う計算 おまけ付き Geogebra




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



三平方の定理




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題
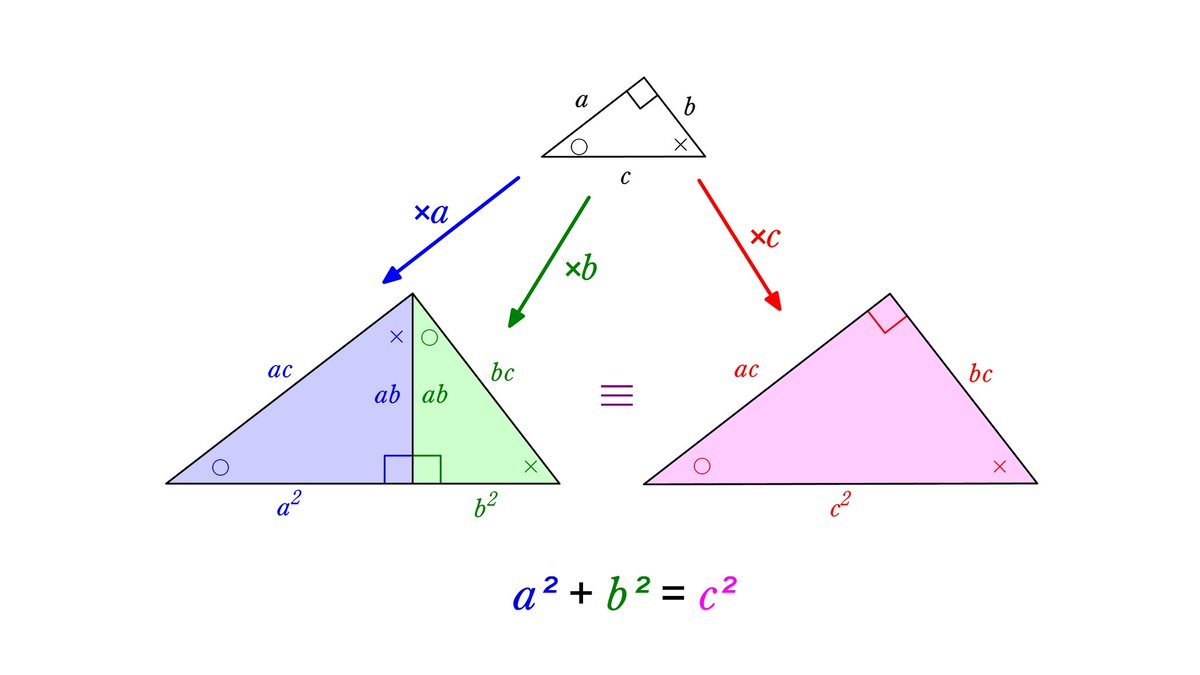



ポテト一郎 三平方の定理 一番好きな証明です




ウケる数学 三平方の定理で解く 地平線までの距離 中日新聞web



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
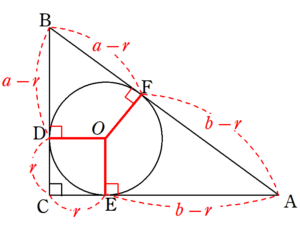



三平方の定理の証明 内接円の利用 Fukusukeの数学めも




三平方の定理の証明と使い方



三平方の定理




三平方の定理 覚えておきたい基本公式を解説 数スタ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理の4通りの美しい証明 高校数学の美しい物語




三平方の定理で ルートがつく計算になるのはなぜですか Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理を直角三角形二つで証明 Youtube
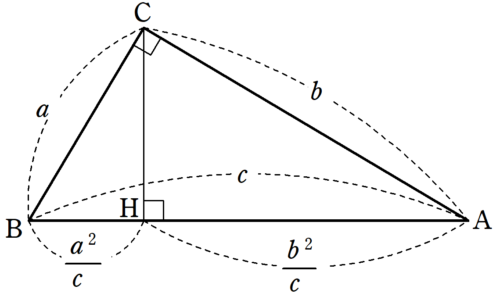



三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




コラム ピタゴラスの定理 江戸の数学




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



1




三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生




三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




Abcの面積を求める問題ですが Aから辺bcに向かって垂線を引いたあと Xと10 Clear




三平方の定理 ピタゴラスの定理 東大合格コム




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理の練習問題10問 解き方の解説 数学fun




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
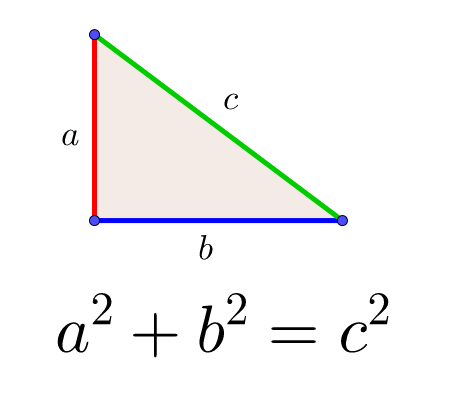



三平方の定理の証明2 4つ直角三角形と真ん中の四角 キソカラ




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
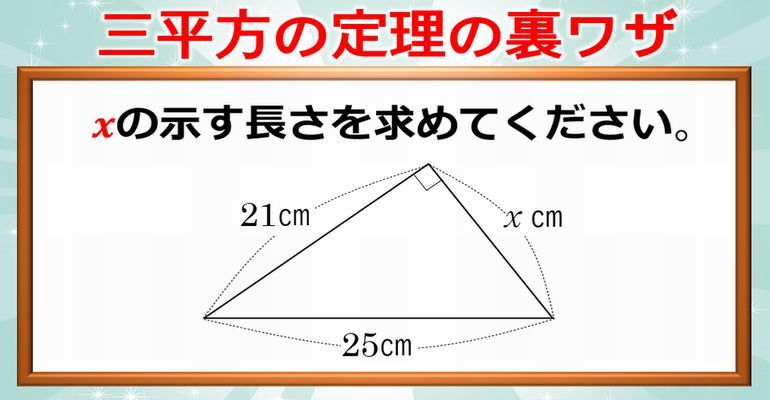



三平方の定理の裏ワザ 賢く解きたい計算の裏ワザ 子供から大人まで動画で脳トレ 楽天ブログ




中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su



三平方の定理




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理の証明と使い方



三平方の定理
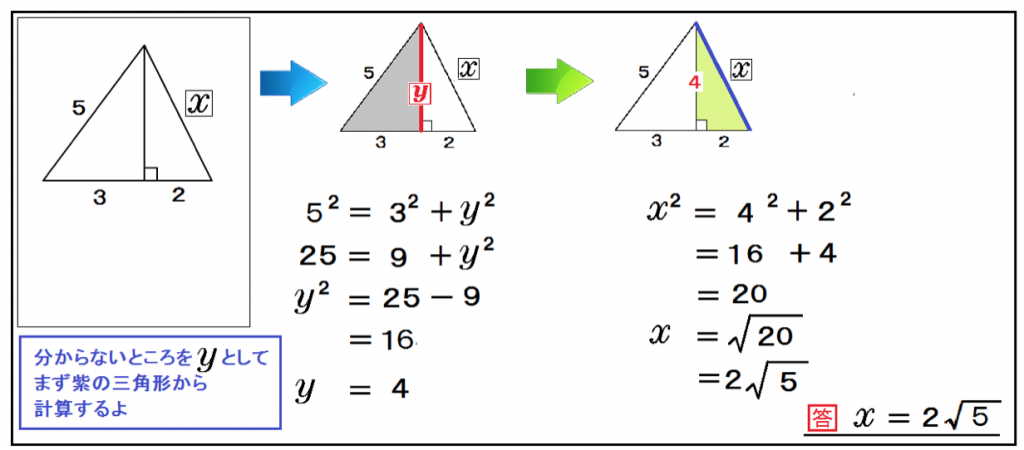



三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




Junior High数学的 中学数学 三平方の定理のキホン 筆記 Clear




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube



Studydoctor三平方の定理の計算 中学3年数学 Studydoctor



ピタゴラスの定理とその証明




三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも




三平方の定理 チーム エン




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿