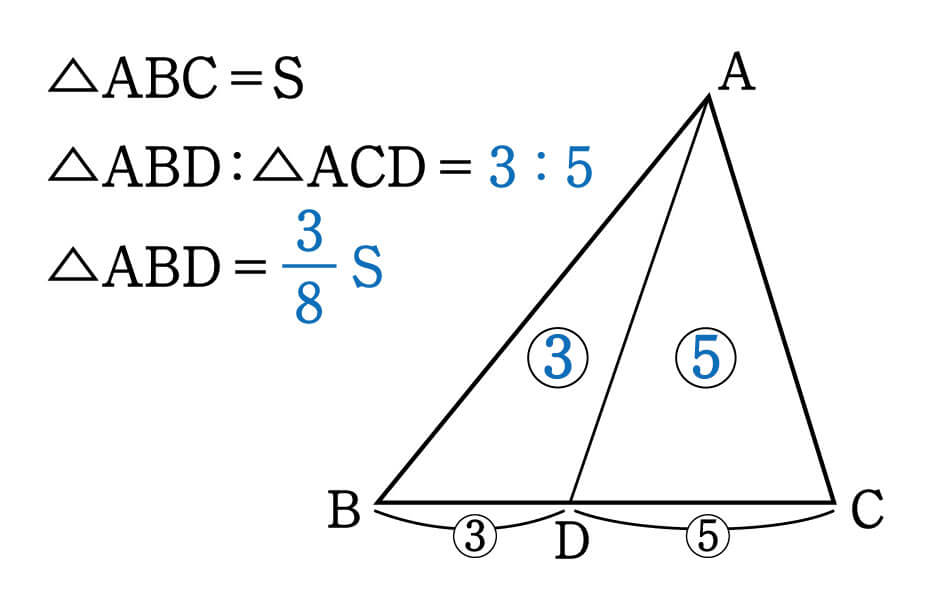
算数図形編 でる度⇒ ★★ 面積比・線分比・相似 面積比を辺の長さで表そう 下の図のように, 辺の長さが4cm,7cmの平行四辺形ABCD があります。よってADDB=AEEC 例それぞれBC//DEである。 8cm 6cm 9cm 7cm x y A B C D E BC//DEより BCDE=ACAE=ABAD 86=x9 6x=72 x=12 86=7y 8y=42 本シリーズは「算数文章題」「算数図形」「国語文章読解」「理科」「社会」があります。 答え・解説 答え 12cm 2 解説 三角形ABCと三角形ADEの底辺の比は, BC:DE=(1+2+1):2= 2:1 面積比も2:1となるので,斜線(しゃせん)部分の面積は, 24 ×1/2= 12(cm 2 )
相似 平行線と線分の比 の分野です 面積比の問題なのですが Yahoo 知恵袋
線分の比と面積比 中学
線分の比と面積比 中学- さて、今回は、中学三年生の数学「相似」という単元の中の「三角形の線分の比と面積の比」の話。例題 上の図で、ADDB=23、BEEC=41である。 BDEの面積は ABCの面積の何倍であるか答えなさい。この問題には何通りかの解き方がありますが、どれも、,セギ英数教室 角木優子 の塾 「角を共有する三角形の面積比は線分の積の比に変換できる」 と覚えておきましょう。 この公式の頻出応用例として, a d e ade a d e と四角形 b d e c bdec b d ec の面積比を求める問題も



相似 平行線と線分の比 の分野です 面積比の問題なのですが Yahoo 知恵袋
相似・線分比と面積比の徹底演習65問 算数徹底演習 中学受験算数の「相似・線分比と面積比」を完璧にするために、全65問の演習プリントを作成しました。 3レベルに分けてありますが、レベルAが必修問題、レベルBがR4や四谷でSS55程度の中堅校、レベルCが難関校レベルになります。 目次 1 PDFファイル(問題・解答解説) さて、この線分比や面積比の問題は 結構ちゃんと割合が分かってないと 意味が中途半端になりがちで 応用がききません。 しかし、この学年の スムーズさは例年でも 群を抜いています。 本当によく理解して、 ついてきてくれています。 さて、このペースでいけば、 夏休み前には円まウ 平行線と線分の比についての性質を見いだし,それらを確かめること。 エ 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解す ること。 オ 相似な図形の性質を具体的な場面で活用すること。
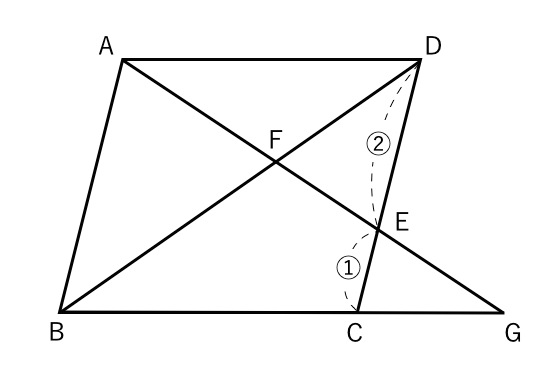
線分の比と面積比中学3年数学 え、1日27円のプロ家庭教師!? <問題> <答えと解説授業動画> 答え (1)3:5 (2)35/6倍 (6分の35) <類題> 動画質問テキスト:中3数学p139 ツイート 中村翔(逆転の数学) 「やり方を知り、練習する。」 そうすれば、勉強は誰でもできるようになり(1) 線分dgの中点を iとする。このとき,線分deと線分 ifの長さの比はde if= 1である。 (2) 線分afと線分bhの交点をjとする。このとき,線分ajと線分hgの長さの比はajhg= 3である。 (3) abcの面積は j ifの面積の 倍である。故に相似な三角形の辺の比は等しくadde=fbbe=13 be=6よりfb=2 線分aeが円oの直径なので、弧aeに対する円周角より∠abe=90°より fbeは直角三角形。 ∴ fbe= 1/2 * fb * be = 6 1 後半 次に fbe gfb = fe fg 2 (fefgが分かれば面積比から gfbの面積を計算できそう・・・)
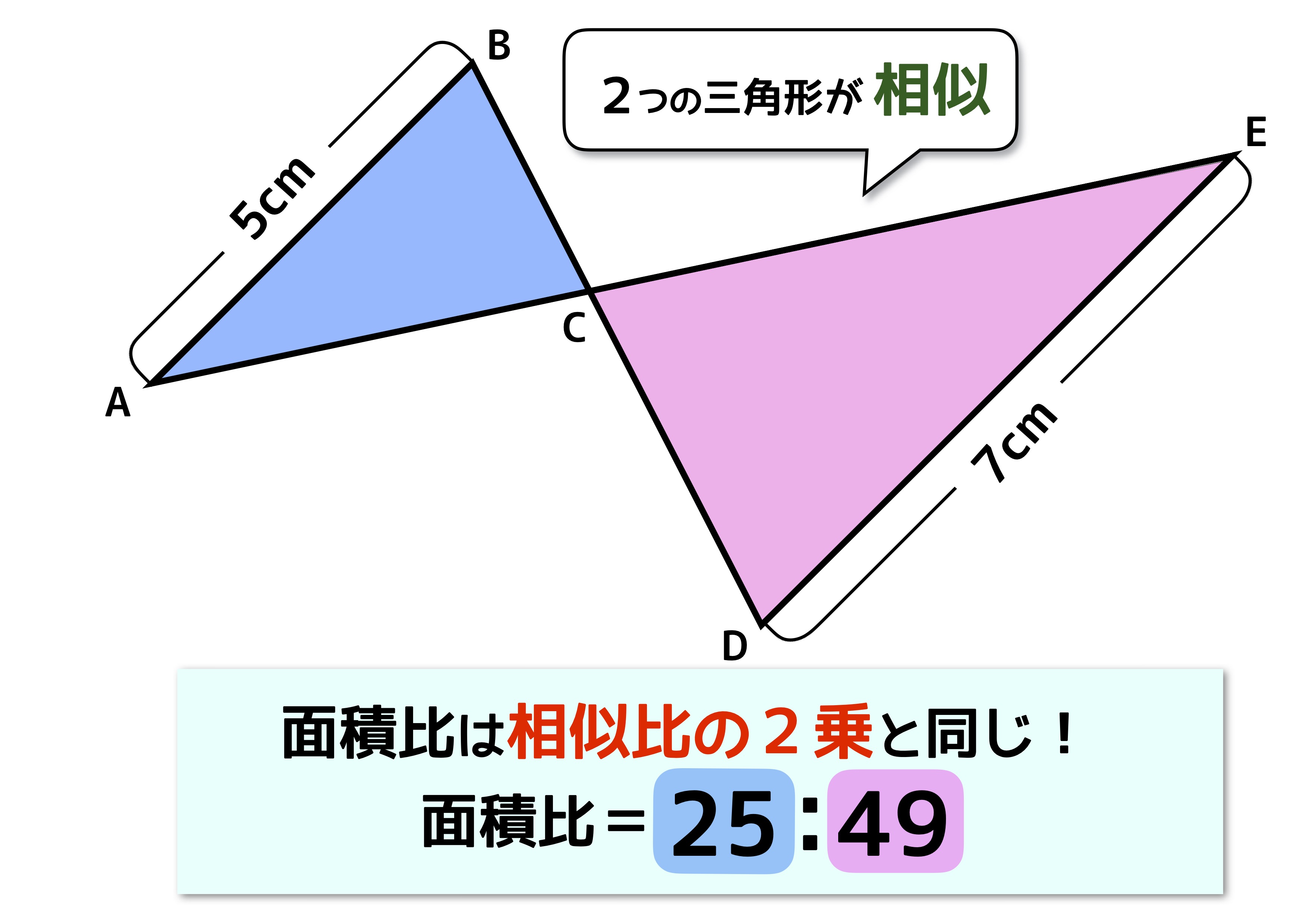
中2で解ける線分・面積比問題(21広島県大問3) スポンサーリンク 中2でも解けるので,今の時期,何か難しめの問題解きたいときにおすすめです。 広島県の全部の問題はコチラ( 広島県ホームページ ) 大問1以外は記事にしました。 ・大問と は を底辺として高さだけを共有しているので、面積比は線分比になります。 最初に求めた三角形の相似の関係から、 の線分比は ですね。 という事になります。相似比・面積比・体積比 ・相似な平面図形において、相似比が $mn$ であるとき、面積比は $m^2n^2$ ・相似な空間図形において、相似比が $mn$ であるとき、表面積比は $m^2n^2$ かつ体積比は $m^3n^3$



Studydoctor線分の比と面積比 中学3年数学 Studydoctor




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
04 「線分比~面積比」の変換を活用しよう! (大分県立・改題) 平面幾何/円 前回に引き続き、半円を題材とした、 「線分比~面積比の変換」 の練習問題です。 必ずと言ってもいいくらい、どこかで見かけたことがある図だと思います。 一般の 相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので 線分比を求められれば面積比を計算できます。 面積比が分かれば体積比を計算できます。 というように線分比が分かるというのは図形問題において後半戦を乗り切るのに重要な事なのです。 よって連比をマスターする事による恩恵は計り知れないと言える




平面図形をマスター 三角形の面積比 応用編その2




北辰塾 情報局 直撃 中学入試問題 第311回 東邦大東邦 平面図形 線分比と面積比
相似 線分比・相似の定理 相似と面積比・体積比 相似 例題 相似_基礎 相似比と線分1 相似比と線分2 相似と線分比1(平行四辺形) 相似と線分比2 中点連結定理1 中点連結定理2 角の二等分線と辺の比1 角の二等分線と辺の比2相似・線分比と面積比 レベルaの25題 問1 右の図でabとcdが平行なとき、ア〜エの長さを求めなさい。 問2 右の図でabとcdが平行なとき、ア、イ、ウの長さを求めなさい。 問3 右の図形はある土地の1:00の縮図です。この土地の実際の面積が何m2 面積比は2乗してやった比の、 1² 2² = 1 4 になるはず! おめでとう! 相似比から面積比を計算できちゃったね。 面積比の公式をつかった問題に挑戦! 面積比の公式でもう1つ問題を解いてみよう。 公式はつかっておぼえるのが一番!




ある2つの三角形の辺の比と面積比について 身勝手な主張




平面図形をマスター 三角形の面積比 応用編その3
幾何の問題に取り組む際に、 「線分比・面積比・体積比の相互変換」 が自由自在に行えるよう、練習を積んでおくことを以前から伝えてきました。その成果を、ちょっと試してみましょう。 問題1ab=3,ac=4で辺bcが最長辺となる直角三角形abcがある。と線分fgとの交点をh、線分beと線分fgとの交点をiとする。 このとき、三角形BGIと三角形EHIの面積の比を最も簡単な整数の比で表しなさい。 (解) FD:AD=3:7 より、 EHI: EAB=3 2 :7 2 =9:49 なので、 EHI=9S とお相似な三角形の面積比は,相似比の2乗に等しくなるので FEB の面積: FAD の面積=9:49 18cm 2: FAD の面積=9:49 FAD の面積は98cm 2 (エ) AFE と AED は高さが等しく,底辺の比がFE:ED =3:4 底辺の比=面積の比となるので, AFE の面積: AED の面積=3:4 42cm 2: AED の面積=3:4 42:x =3:4 比の解き方




高校数学a 三角形の面積と線分の比 練習編 映像授業のtry It トライイット
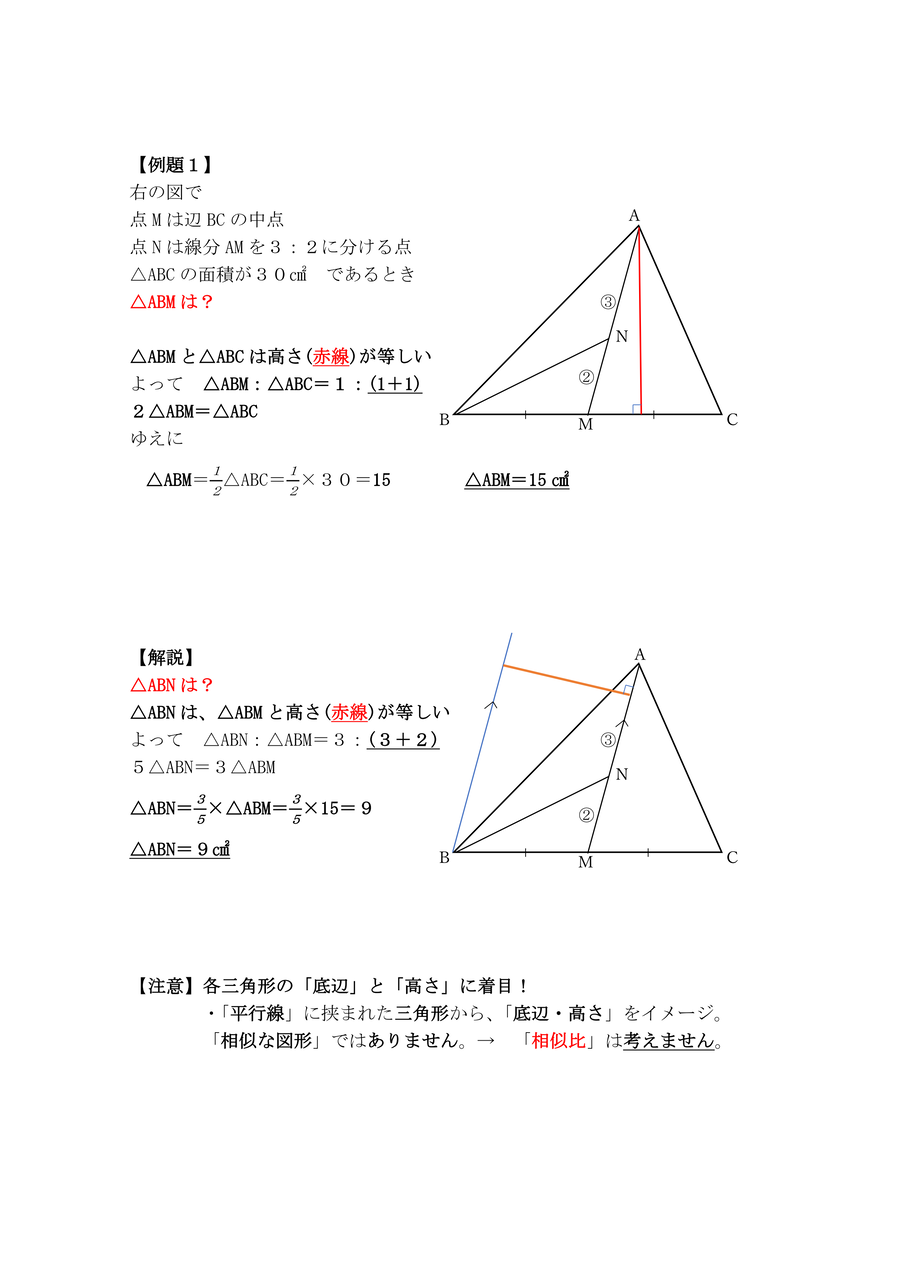



中学校数学 証明のコツ 面積比 体積比
相似比がabのとき 面積比=(a×a)(b×b) 体積比=(a×a×a)(b×b×b) 例えば長方形の面積は「たて×横」なので、たての長さも横の長さも2倍になれば「2倍×2倍」になるという理屈です。 同じように考えて、例えば直方体の体積は「たて×横×高さ」な 図形と相似の最終回です。 計算に関する問題が中心となりますが、 特に面積比・体積比はしっかりと練習しておきましょう。 11.角の二等分線と線分比 eclus13 215K subscribers Subscribe 角の二等分線と線分比 中3数学 図形と相似11基本的な立体の相似の意味と、相似な図形の相似比と面積比、および体積比の関係について理解し、問題でくり返し練習します。 面積の比と体積の比(1) ⇒ 答え 面積の比と体積の比(2) ⇒ 答え 面積の比と体積の比(3) ⇒ 答え 面積の比と体積の
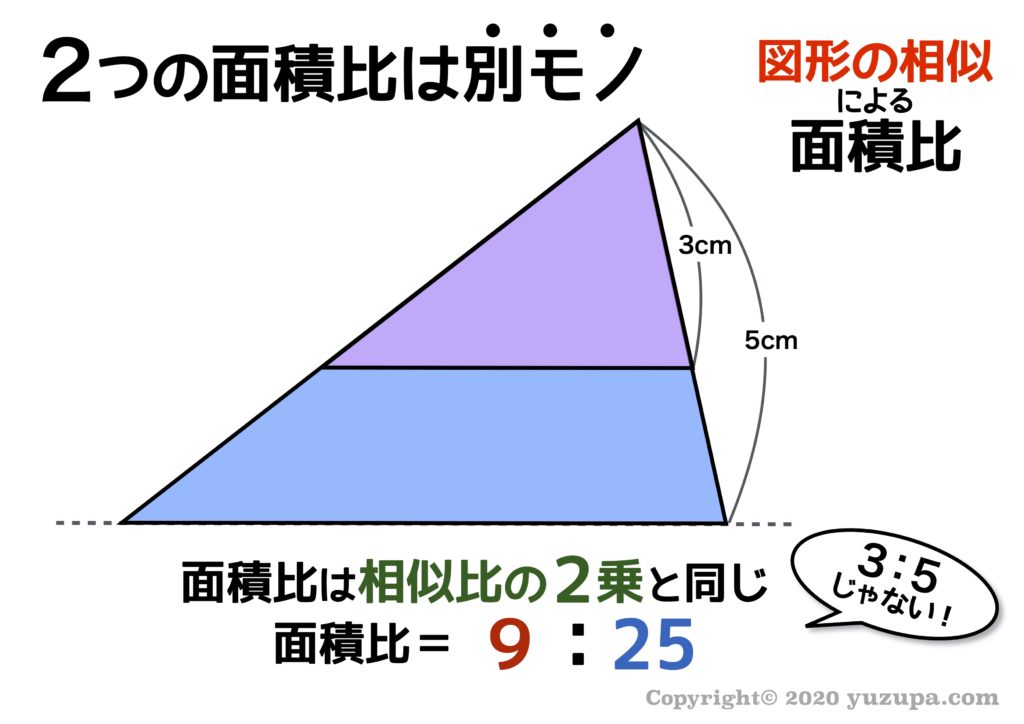



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学
線分比と面積比の関係は,中学受験でもしないと,中々知らないと思われます。 上図のことを知っていると,人生大分楽になります。 じゃあ,これを関数でどう活かすのかというと。 どうやってAD:DB=3:1を出すのか?それは,x座標の差,またはy座標の差が,そのまま線分比とな線分比と面積比 1線分比と面積比 右の図のように,ßabc と点 d があ るとき,次の等式が成り立つ。 ßabd:ßadc = bd:dc (例) 右の図のように,ßabc が あり,点 d は辺 bc 上の点であ る。bd:dc = 2:3 のとき, ßabd とßadc の面積比似条件,平行線と線分の 比についての性質,相似 比と面積比及び体積比 の関係の意味などを理 解し,知識を身に付けて いる。 ⅥⅥⅥⅥ 指導と評価の計画指導と評価の計画 単 元 題材 指導目標 主な学習活動 時 数 《言語活動系統 表》との関連 相 似 な 図 形 (22




中3 20 1 線分比と面積比 1 Youtube




平面図形をマスター 三角形の面積比 応用編その2
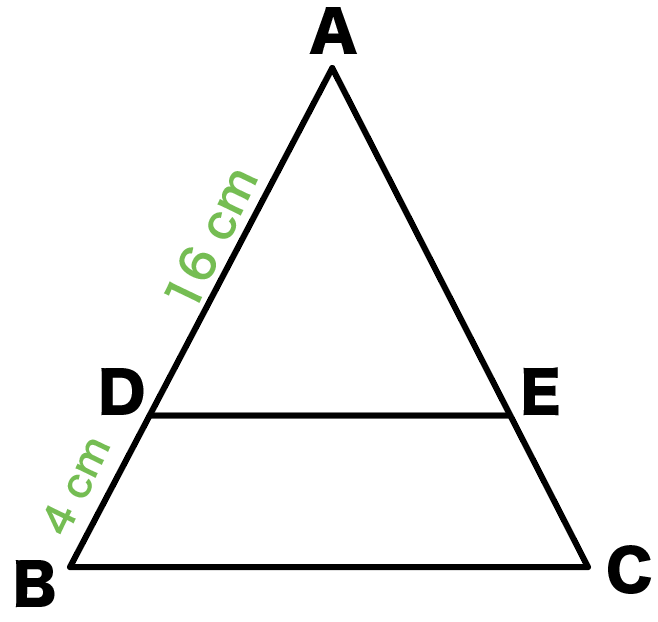
線分の比では、ac:cbというただ1つの比を求めればよかったのに対し、 三角形の面積比は2つの比 を扱います。 そのため、通常の比の計算より少しむずかしく感じるかもしれません。面積比は1 2 :3 2 =1:9 (2) edfの面積をsとおき,各部分の面積をsを使って表す。 (1)より,( bcf の面積)=9s edf と ecf で,それぞれの底辺をdf,cf とすると高さ は共通なので, edf と ecf の面積比は底辺の比1:3 と等しくなる。 edf の面積がs なので,STEP 1 : A B E ∽ D C E A B D C = 9 c m 12 c m = 3 4 (相似比) POINT:対応する線分の長さの比は、すべて等しい STEP 2 : B C D ∽ B E F ( A B D ∽ E F D でもOK) ③ ④ ③ B C B E = ③ ④ ③ = 7 3 (相似比) 3 7 = x 12 これを解いて、 x = 36 7 1:24 例題 2 A D / /




高校入試数学 入試によく出題される代表的パターンまとめ




相似 平行四辺形と面積比の問題を徹底解説 数スタ
比べる三角形が相似でなくても、高さが等しければ 底辺の長さの比が、そのまま面積比となります。 問題を解いていく上で これら2つの特徴を利用していくことになるから しっかりと覚えておいてくださいね! 台形の面積比問題を解説① 線分の比と平行線 (平行線と線分の比の逆) 上の「平行線と線分の比の定理」の逆も成り立てば、もっと鋭い武器になりますね! すなわち、「ここと、ここの比が同じならば、2直線は平行である!」と言いたいですね! 「~ならば、~である」の逆、「~であるならば、~である」は当然に2つの線分の交点の位置ベクトルや 内分比を求める裏技(教師用) 札幌東高校 佐藤 清 はじめに ベクトルの単元のいわゆるst問題を扱ったときに,ふとしたはずみで下の問題のような2つの線分の交点の位置ベクトル,あるいは各線分の内分比を求める簡易的方法(裏技)に気がついたので今回




面積比
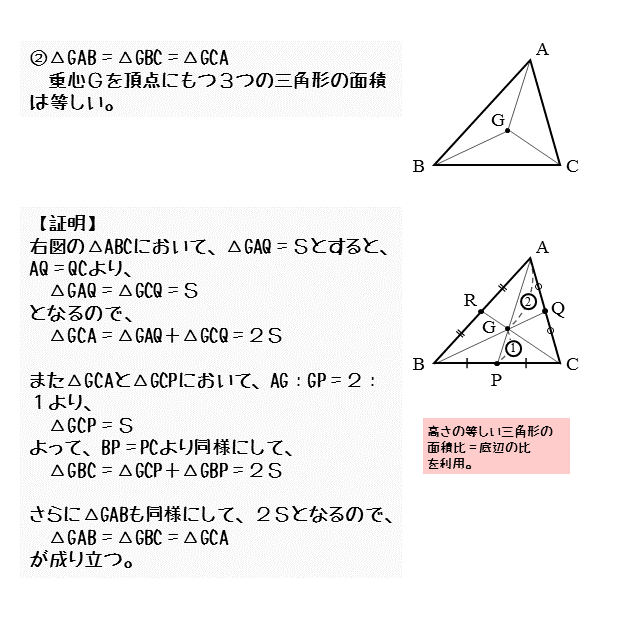



図形の性質 重心について 日々是鍛錬 ひびこれたんれん
台形abcdがあり、上底adと下底bcの比は2:3です。 台形の面積が50cm 2 であるとき、 aobの面積はいくつでしょうか? という問題です。 問題文には‟面積比"という言葉が使われていませんが、2つの異なる図形の面積を比べる問題なので、これも面積比のパターンの1つです。 高さが共通の隣り合う三角形の面積比は底辺比に等しい。 これが最重要の型のひとつです。 相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa 2 :b 2 になる という性質があります。 これがおぼえるべき、2つ目の型です。 さきほど示した17種類の内、14個は①と②を




高校入試対策数学 面積比に関する対策問題 Pikuu




平面図形をマスター 三角形の面積比 応用編その2
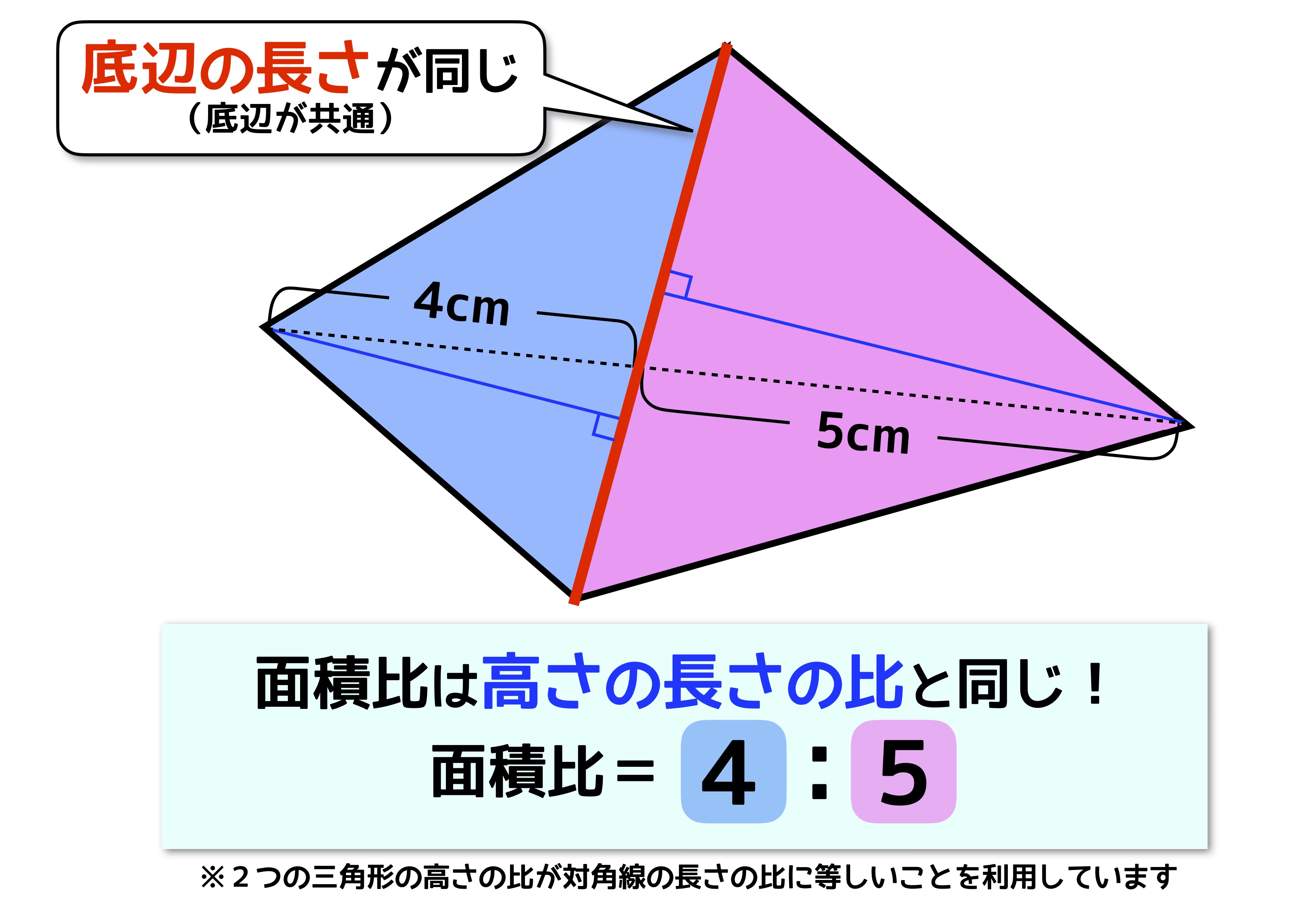



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
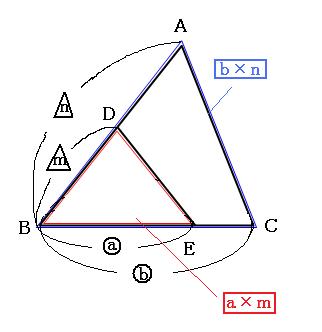



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める
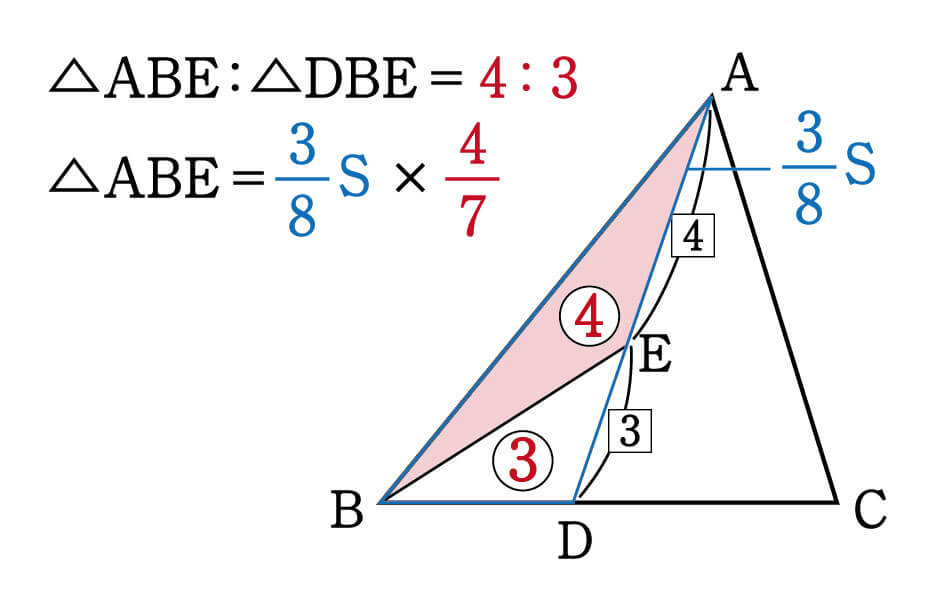



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校数学a 三角形の面積と線分の比 練習編 映像授業のtry It トライイット




39 面積比から線分比を求める Youtube




三角形の面積比にまつわる公式たち 高校数学の美しい物語
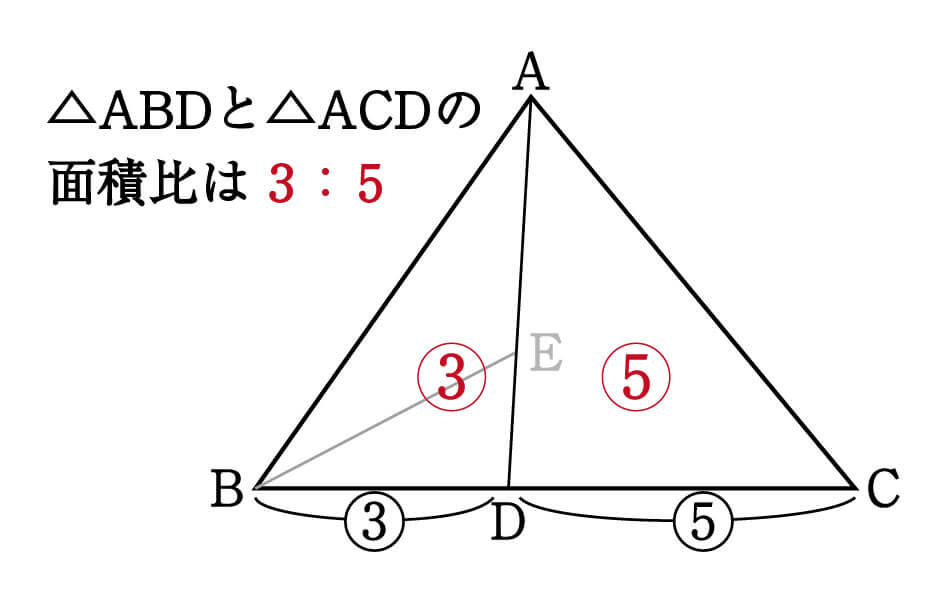



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問



3
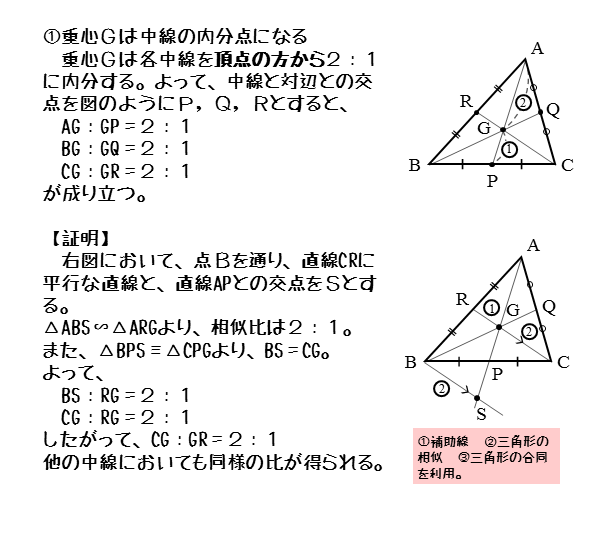



図形の性質 重心について 日々是鍛錬 ひびこれたんれん



面積比は相似比の2乗で表せますが 面積比と線分比はどうな Yahoo 知恵袋




相似比と面積比 中学3年数学 Youtube




北辰塾 情報局 直撃 中学入試問題 第307回 都市大付属 平面図形 線分比と面積比
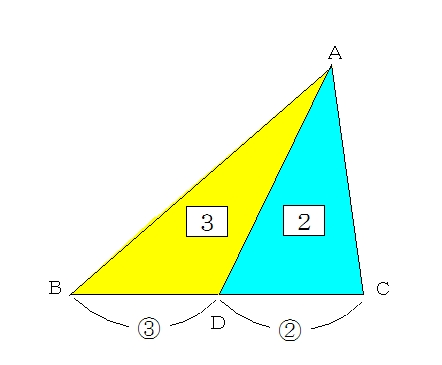



辺の比と面積比



1
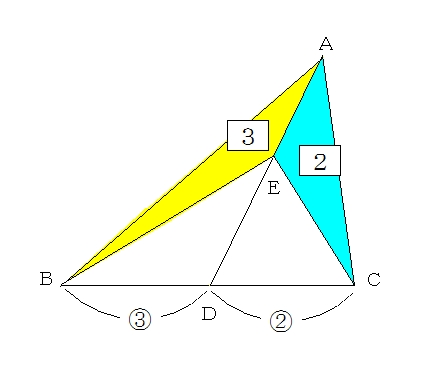



辺の比と面積比
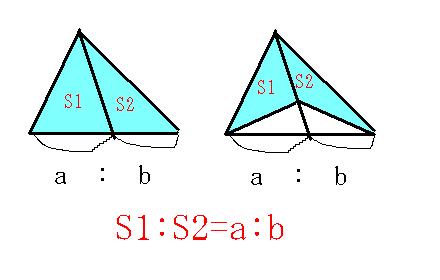



線分の長さの比 1 受験勉強のコーヒーブレーク




相似の面積比を求める問題 上級編 Youtube
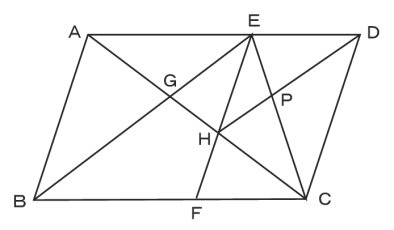



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より




高校数学a 三角形の面積と線分の比 例題編 映像授業のtry It トライイット



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor
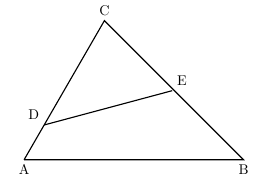



線分比と面積比の問題の解法 夢を叶える塾
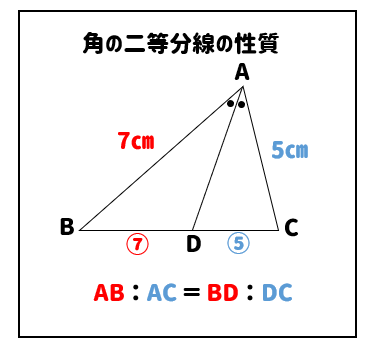



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ



1




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ
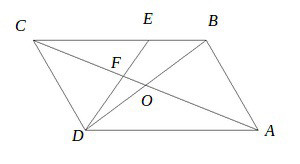



線分比と面積比 Kojinkai




チェバ メネラウスの定理と三角形の面積比




平面図形の苦手を解消 三角形の面積比 基本編




辺の比と面積比 基本編 Youtube




線分の比と面積比 中学3年数学 Youtube



芝11 5 平面図形 線分比や相似を利用して面積比を求める問題 気まぐれ解説カフェ 仮




三角形の面積比 数学の偏差値を上げて合格を目指す




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
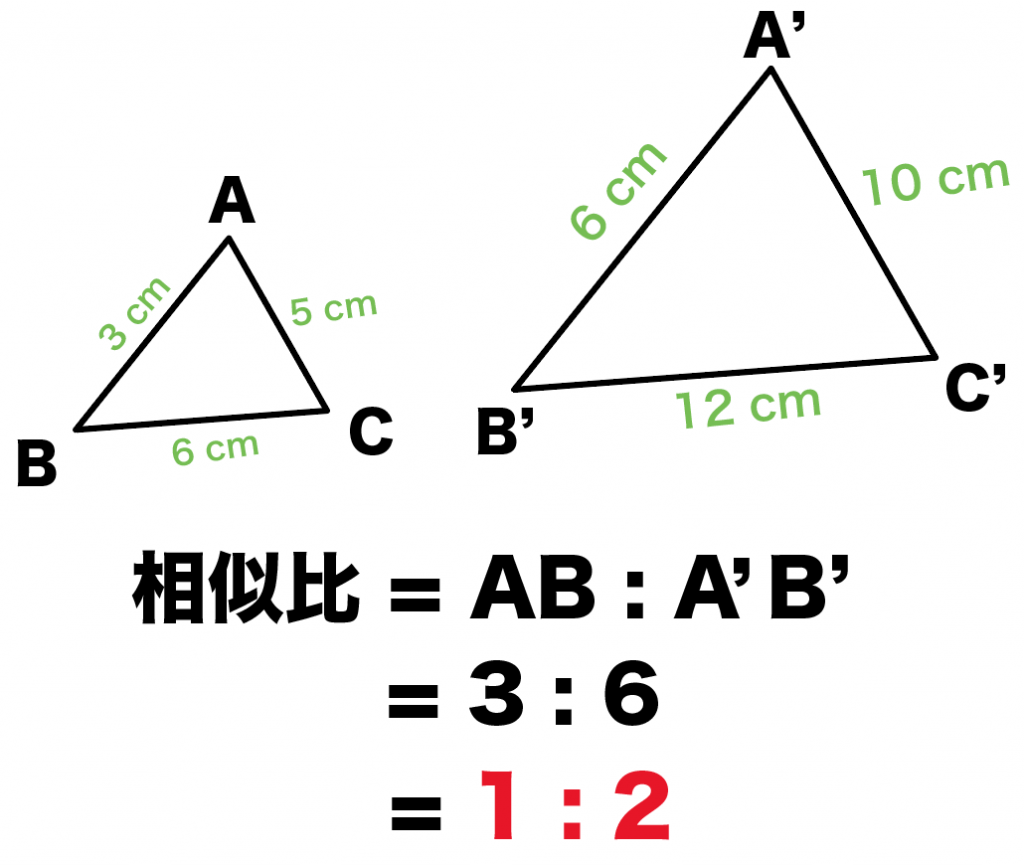



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
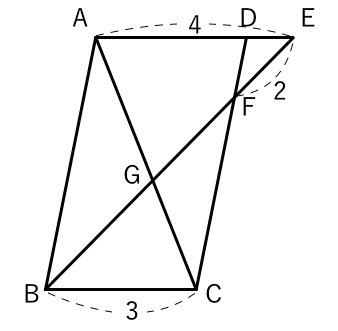



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
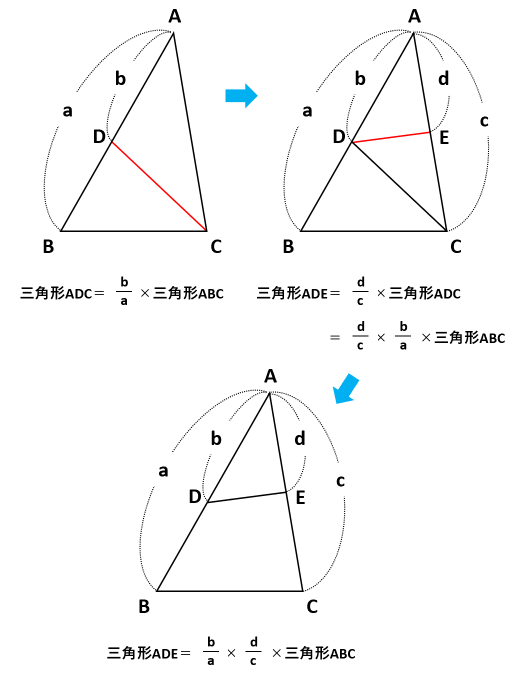



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




応用 ベクトルの等式と三角形の面積比 なかけんの数学ノート




三角形の面積比にまつわる公式たち 高校数学の美しい物語




平面図形をマスター 三角形の面積比 応用編その3



相似 平行線と線分の比 の分野です 面積比の問題なのですが Yahoo 知恵袋




線分比と面積比 鷗友学園女子 H18大問3
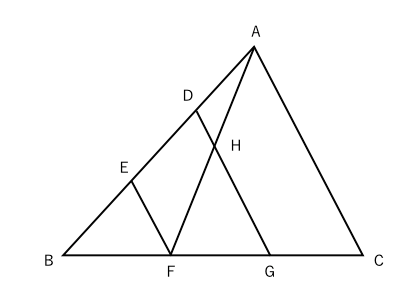



面積が何倍かを求める問題 応用編 苦手な数学を簡単に




数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki




中学校数学 証明のコツ 入試で差がつく 面積の比 体積の比 を得意にできる教材




中3 20 2 線分比と面積比 2 Youtube




辺の比と面積比問題 考え方1 Youtube
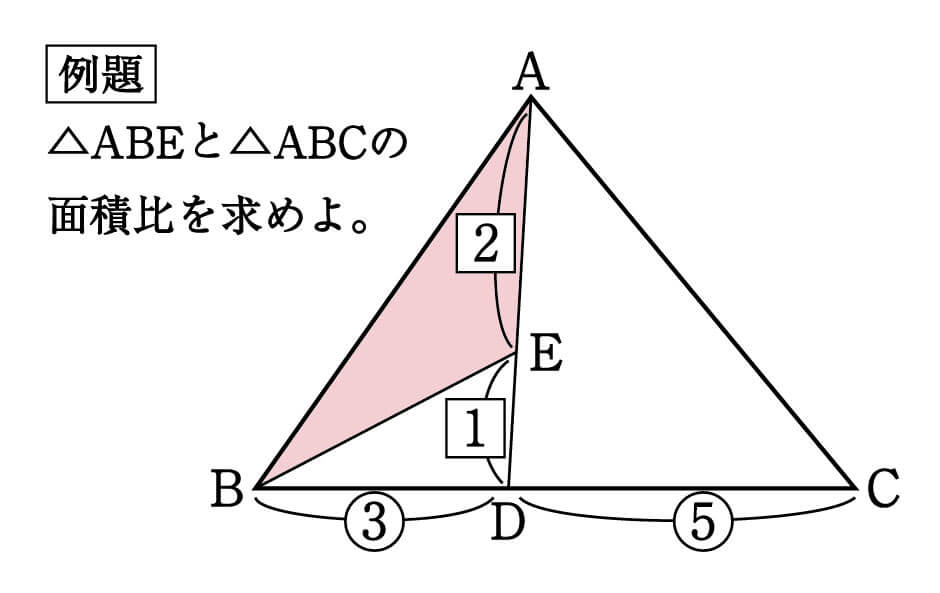



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
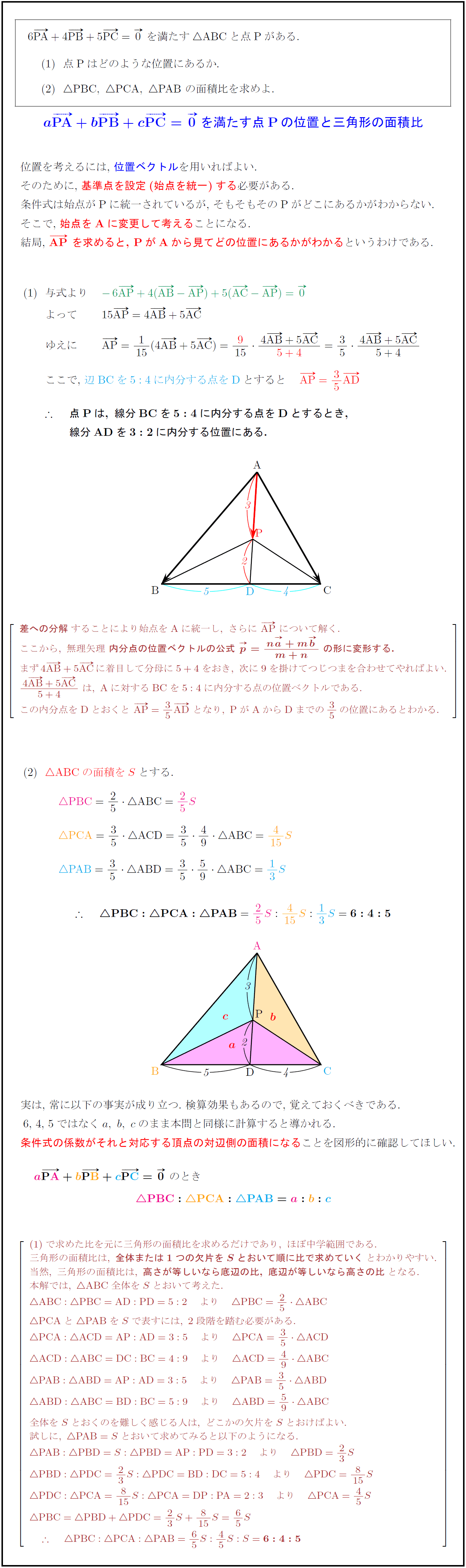



高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
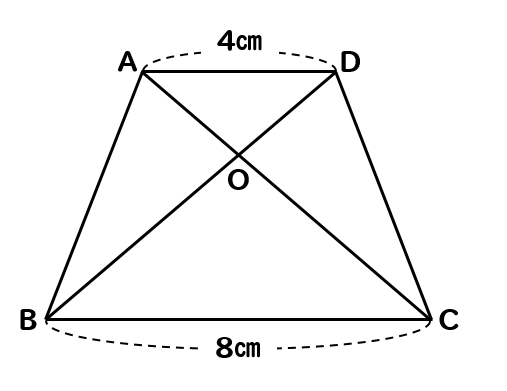



相似 台形と面積比の問題を徹底解説 数スタ



第5章21 面積の比と体積の比 平方四辺形の相似比と面積比 フロントエンドなブログ
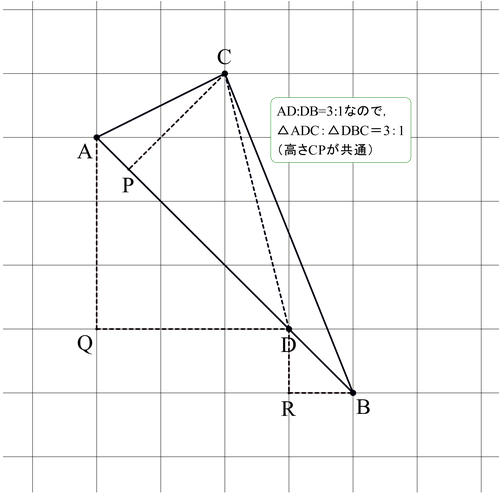



線分比と面積比 クソオリジナル問題 高校入試 数学 良問 難問



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中3数学線分比と面積比 体積比解法質問 写真の図形において 問題文よりab Yahoo 知恵袋



2つの球の半径がそれぞれ5cm 2cmのとき相似比表面積比体積 Yahoo 知恵袋



算数 線分比と面積比 数学 中学受験専門 ともや塾




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




Fines 高校受験対策講座 数学 線分比と面積比 Youtube




角の2等分と線分の比 高校数学の無料オンライン学習サイトko Su




面積比 2つの三角形で高さが同じときの面積比 身勝手な主張



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




メネラウスの定理を面積比 線分比 で証明 Http Club Pep Okwave



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



1




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



相似 図中の線分の比 面積を求める 子供に教える算数のツボ



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ The 2nd
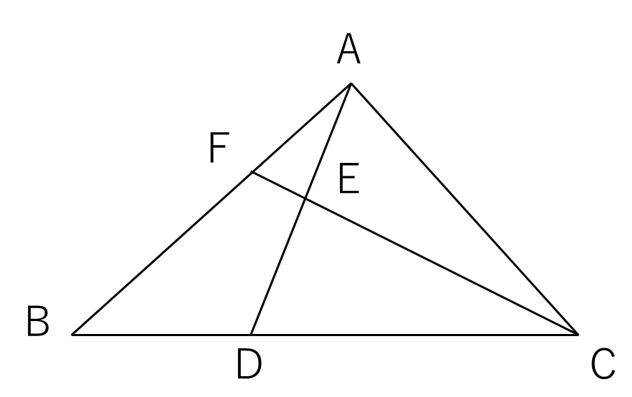



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




線分比 面積比 体積比 数学カフェjr



高校入試数学 面積比のポイントと練習問題
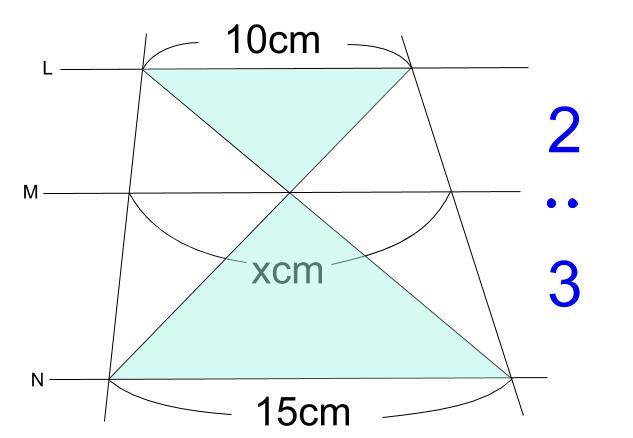



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
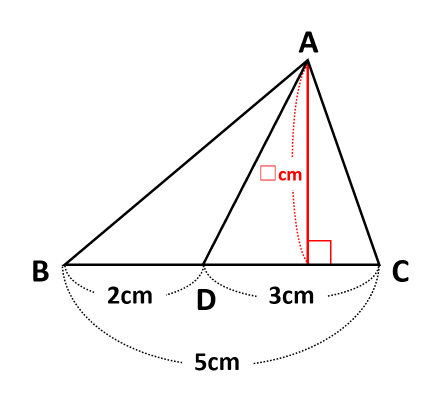



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
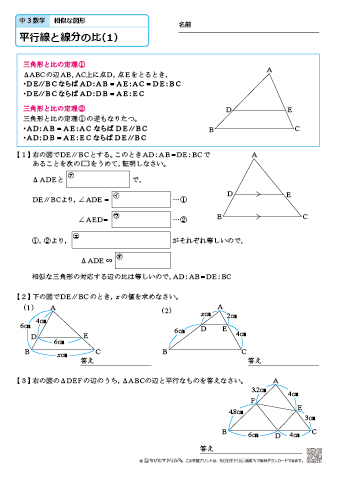



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
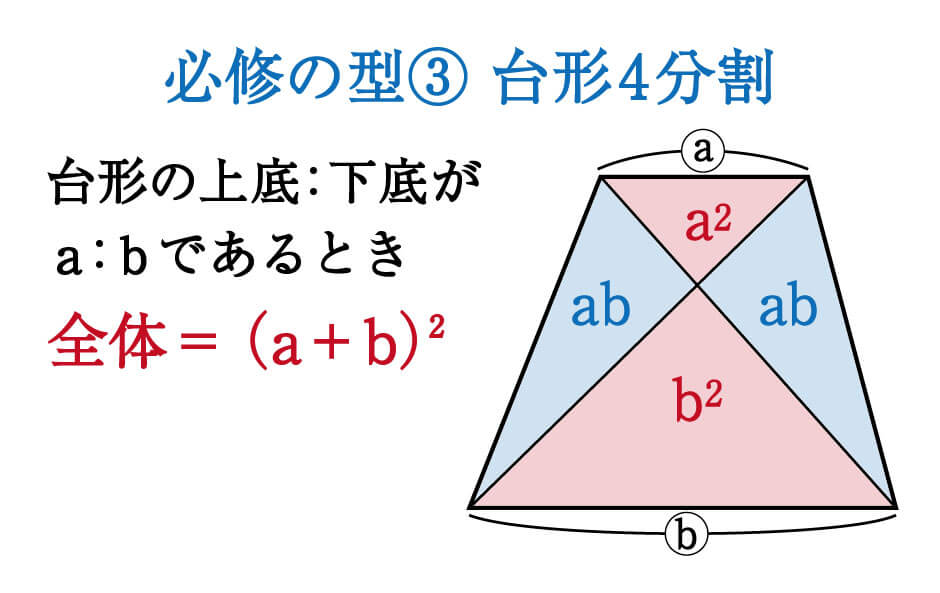



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




相似比は の部分でルートが出てくる意味がわかりません Clear




平面図形をマスター 三角形の面積比 応用編その3




この問題教えてください 線分比と面積比のところです Clear
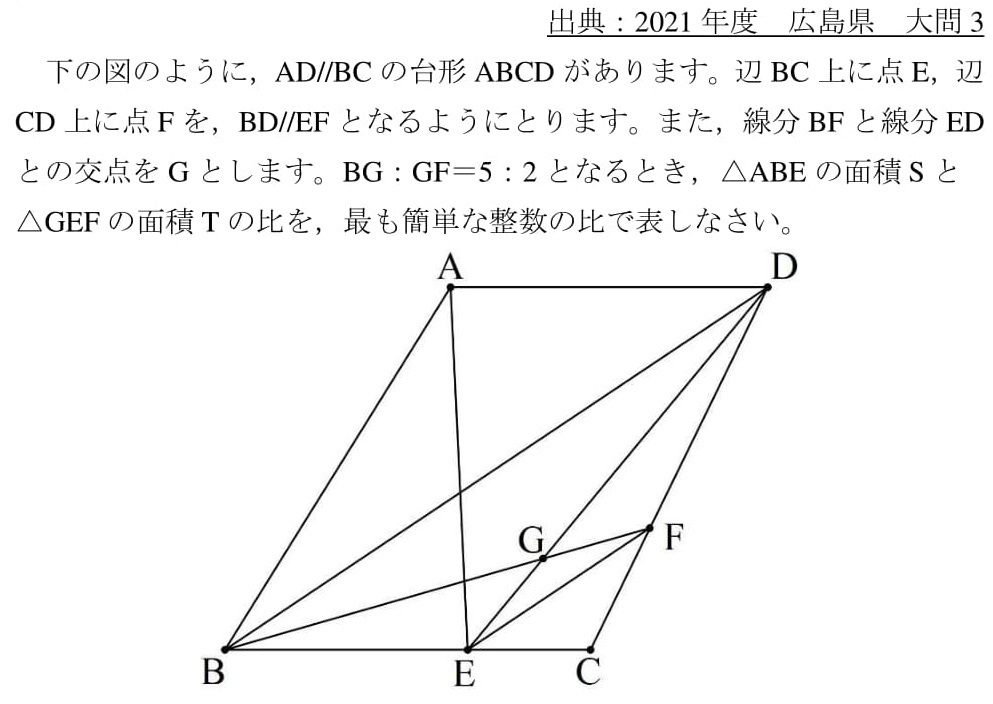



中2で解ける線分 面積比問題 21広島県大問3 高校入試 数学 良問 難問




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor



0 件のコメント:
コメントを投稿