
平方根 4 有理数と無理数 バカでもわかる 中学数学
ルート2、ルート3、ルート5、ルート6の値(小数点以下30桁)と覚え方 ルート2 (一夜一代に夢見頃) 040 167 249 ルート3 1735 (人並みにおごれや) 677少数や分数を含んだ数式の展開にも対応しています。 約分の電卓 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。 通分の電卓 分数を通分できる電卓です。
ルート 分数 少数
ルート 分数 少数-2/3×√と項を分けて考えれば それぞれ少数へと計算して 15×943=1415 と答えが出ます ルートを含む分数はどうやって小数の形にする帯分数を入力する場合は、整数部分を入力してから、「と」ボタンで分母を入力、分母入力後に「分」ボタンで分子を入力。 上側スクリーンが帯分数表示、下側スクリーンが仮分数表示です。 分母を0にすることはできません。 0で割るとエラーになります。
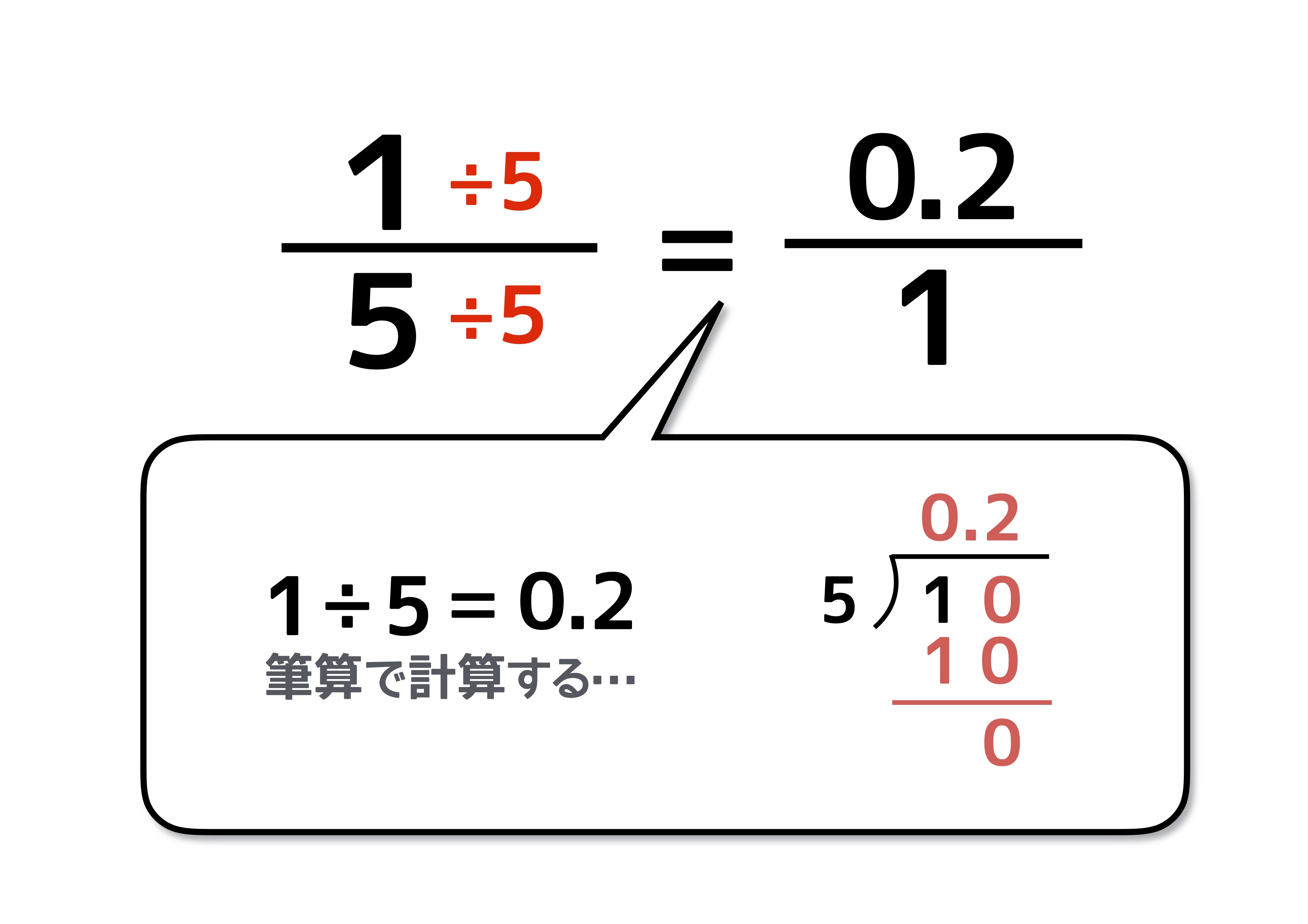
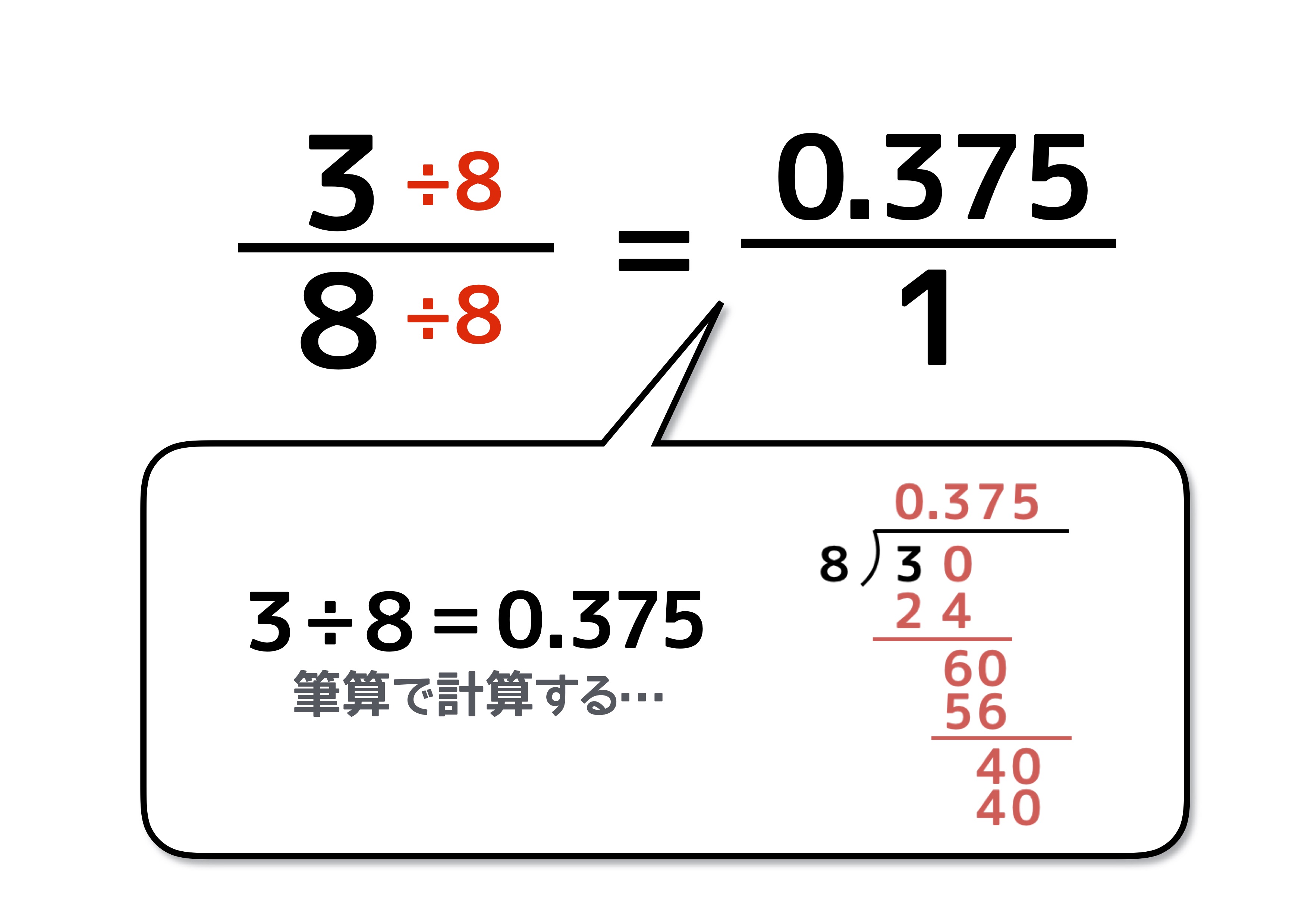
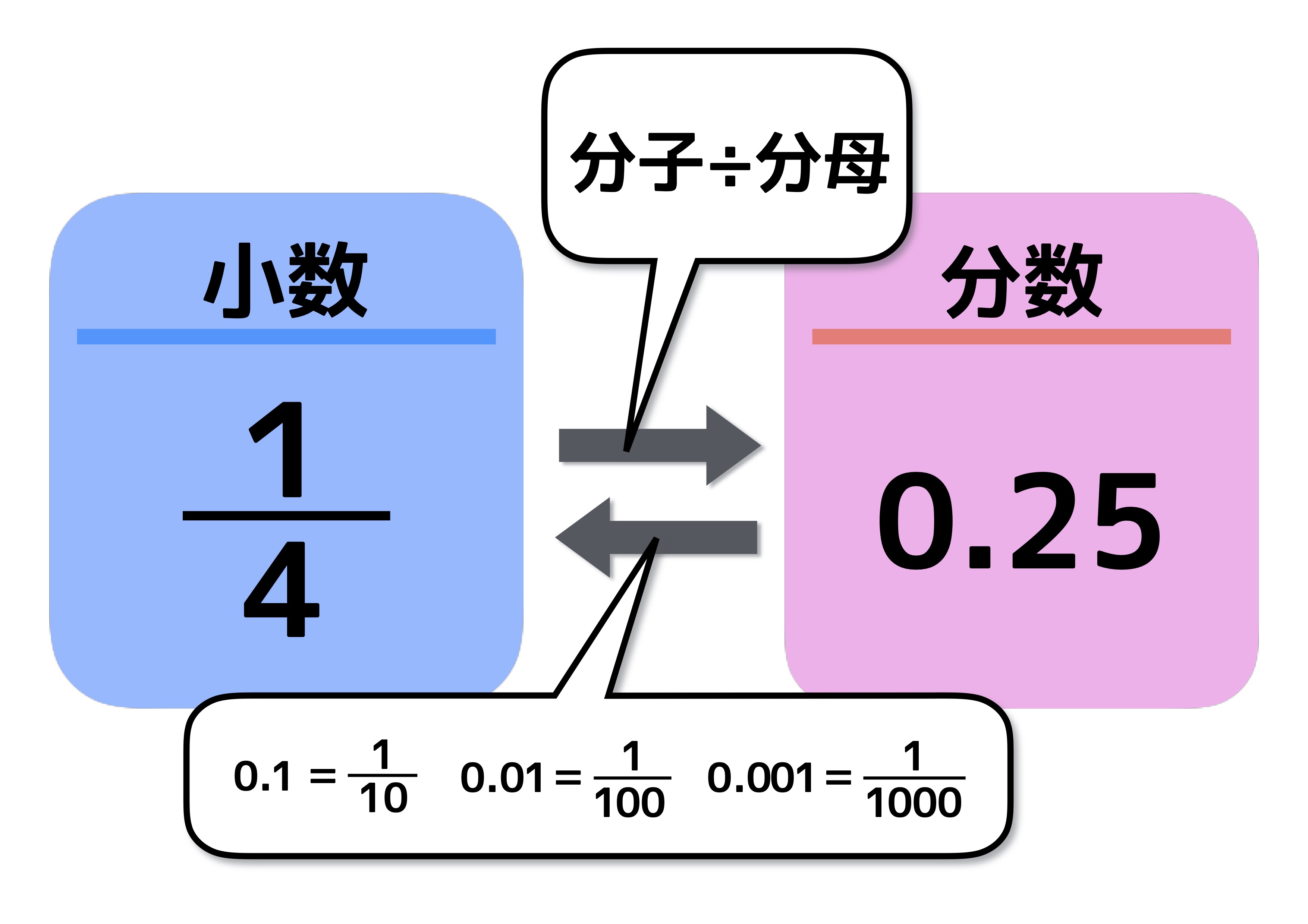
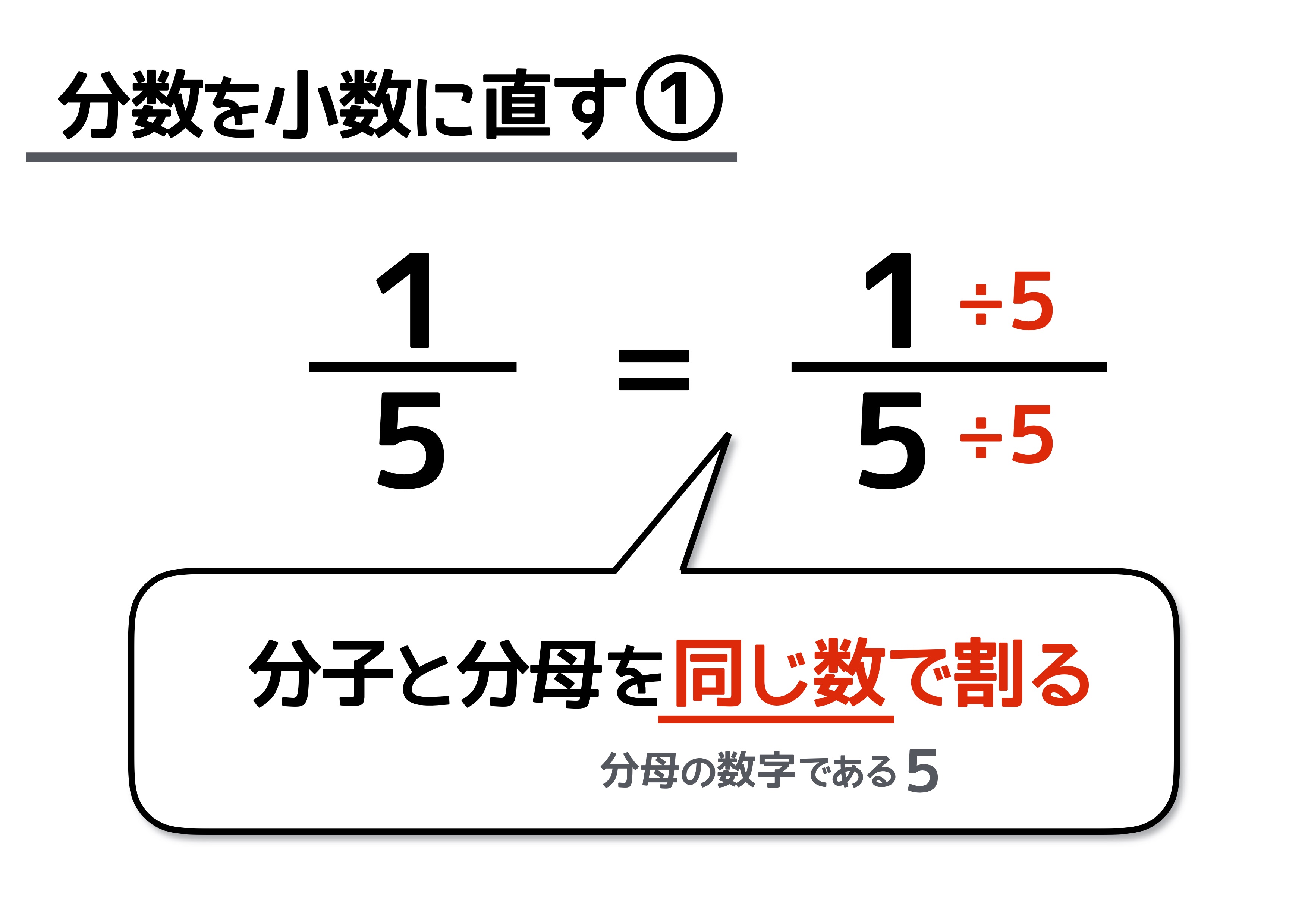
分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ
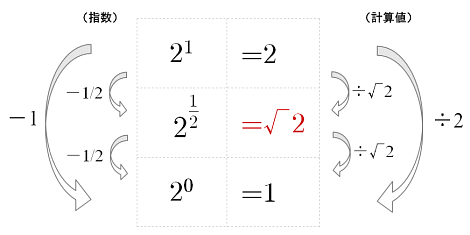
小数を分数に変換する 小数から分数への変換には、けたの値が重要となります。分数の分母が、けたの値となります。また、小数点以下の桁が分子となります。 例えば、 という指数があるとしましょう。 指数の を分数に変換する必要があります。 小数点第2位(100分の1の位)まで続いている ルート(根号)をはずす問題 だ。 これは文字通り、 平方根を「√」を使わないで表す問題だね。 ルート(根号)のはずし方がわかる2つのステップ 今日はこの、 ルート(根号)の外し方 を解説していくよ。 2ステップで外せちゃうんだ。 ルートの中身 約分ができるときは先に約分をして、ルートの中の数をより小さくしておくと計算が楽になります。 ・ ルートの掛け算の計算の仕方のコツって? 次に整数掛けるルートのついた分数の計算をしてみましょう。 (3) 3×√2 3 3 × 2 3 この場合も今までのルート
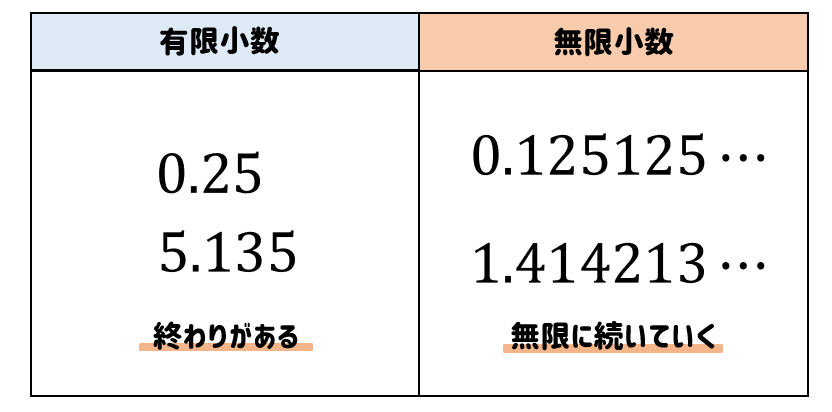
√6のようなルートを少数に直す方法はなんですか?。 中学校 締切済 教えて!goo 少数のルート、分数がまじったこの式の計算が分かりません。 何度挑戦してみても、分母10になりません。 この答えになる過程を詳しく教えていただけないでしょうか。 数学に詳しい皆様宜しく お願い致します。循環小数を分数に直す方法は「循環小数の例と分数に直す方法」にて詳しく解説しています。 無理数とは? 一方で、 「分数で表せない数」 を無理数といいます。 無理数だと判断するのは簡単で、ルートや\(\pi\)などの循環しない小数が無理数です。
ルート 分数 少数のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 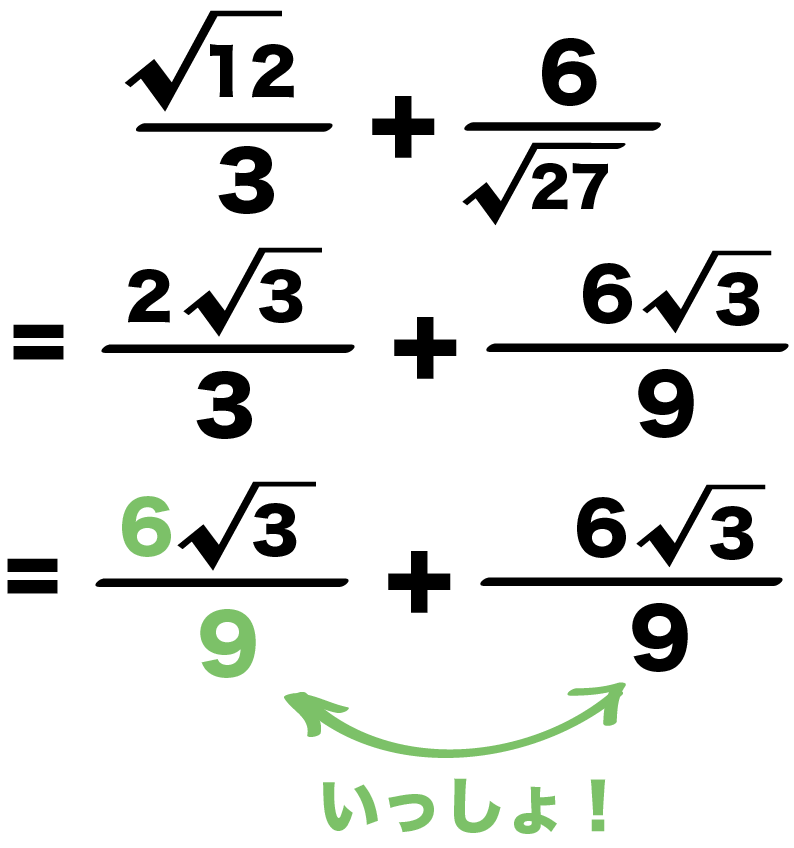 | |
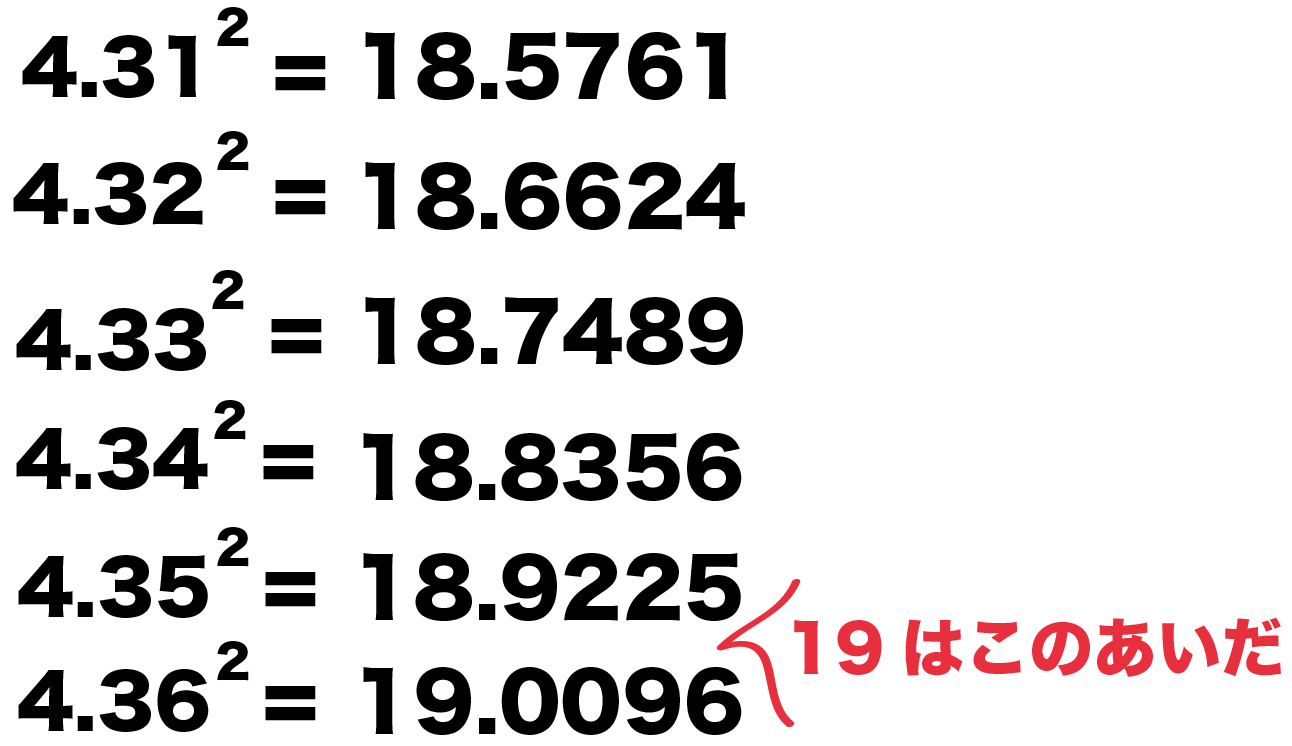 |  | |
 |  | |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | 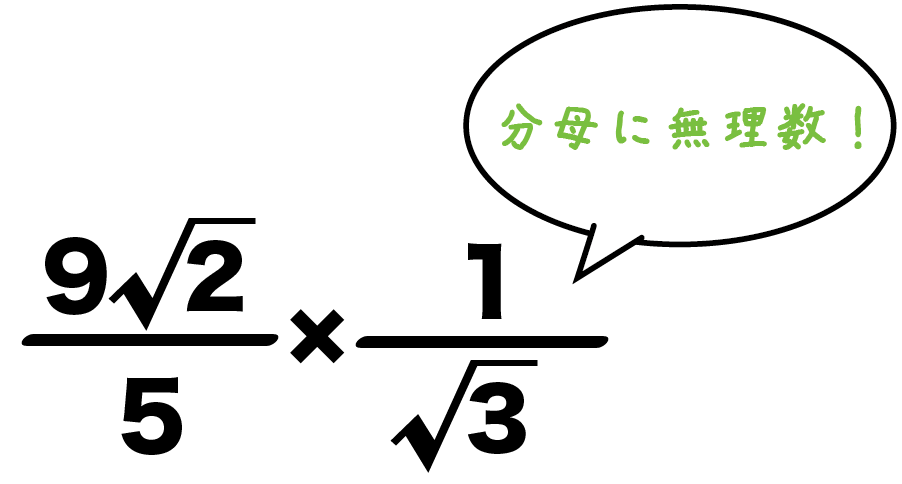 |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
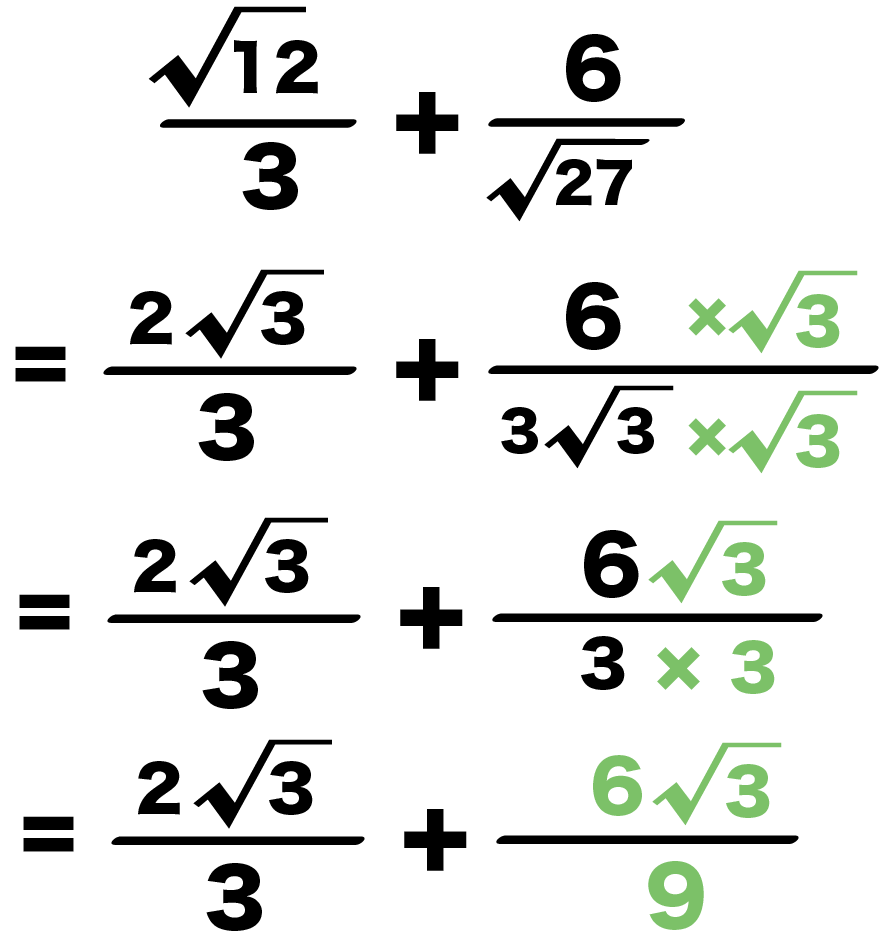 |  |  |
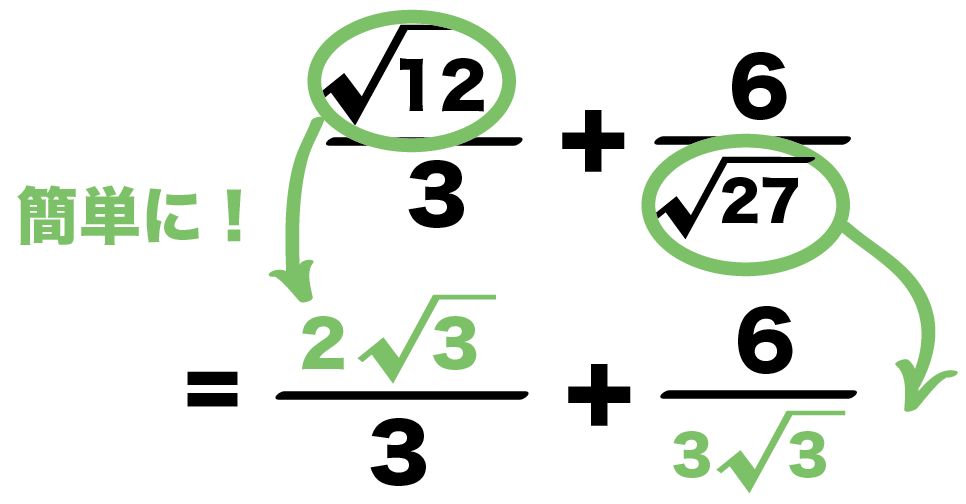 |  |  |
「ルート 分数 少数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 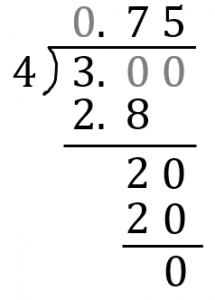 |
 |  |
最後に、ルートをもっと簡単にできるか挑戦。 ルートの中身はいちばん簡単にすべきだからね。 例題の計算をみてみると・・・ ・・・ん!? (2)のルートはもっと簡単にできそうじゃないか?? 中身の147を素因数分解すると、 147 = 3×7の2乗 になってる。①ルートの中身を簡単にする 分数を書くときは \(\dfrac{6}{4}=\dfrac{3}{2}\) のように可能な限り「約分」をしますよね。 それと同じで、平方根を使って数を表すときは ルートの中身を可能な限り小さな自然数 にします。





0 件のコメント:
コメントを投稿